H29年 国家一般職(高卒 技術) No.11 物理　解説

　問 題　　　　　

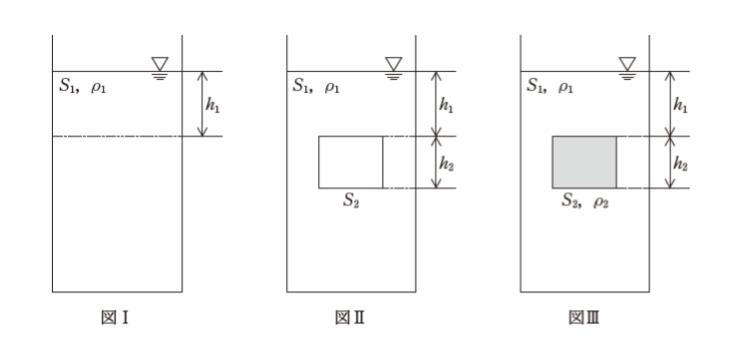
水圧に関する次の記述の㋐，㋑，㋒に当てはまるものの組合せとして最も妥当なのはどれか。ただし，大気圧及び水の密度をそれぞれ P₀，ρ₁ とし，重力加速度の大きさをg とする。

「単位面積当たりに受ける力を圧力といい，水中で物体が受ける圧力を水圧という。図Ⅰのような水を入れた断面積 S₁ の容器における深さ h₁ の面が受ける水圧は，高さ h₁ の水柱の重さによる圧力と大気圧の和で表されるため，力の釣り合いより ㋐となる。

図Ⅱのように，図Ⅰにおける深さ h₁ の面を上面とする，高さ h₂，底面積 S₂ の直方体部分について考えると，上面が受ける力の大きさは，水圧が深さによって異なるため，下面が受ける力の大きさより ㋑ だけ小さくなる。

図Ⅲのように，底面積 S₂，高さ h₂，密度が ρ₂ の直方体を沈めたとき，この直方体が水から受ける力の大きさは ㋒であり，これがこの直方体に作用する浮力となる。」

 

 

 

 

 

　解 説　　　　　

㋐ ですが
「水柱の重さ」は、「体積 × 密度」です。
水柱の体積は 「S₁ × h₁」です。よって、水柱の「重さ」は S₁ × h₁ × ρ₁ です。

「水柱の重さによる圧力」は、「重さを力にして」、「表面積で割り」ます。 つまり、（S₁ × h₁ × ρ₁）× g ÷ S₁ = h₁ × ρ₁ × g です。

大気圧は P₀ とあるので、選択肢に合わせれば
㋐は ρ₁h₁g + P₀ です。正解は 1 or 2 です。

㋑ですが
「力の大きさ」が聞かれているため「圧力×表面積」になっている必要があります。選択肢における「ρ₁h₂g」は、「高さ h₂ の水柱の重さによる圧力」を表しています。そのため、それに S₂ をかけた「ρ₁S₂h₂g」が正解です。

以上より、正解は 2 です。