公務員試験 H29年 国家一般職(土木) No.17解説

　問 題　　　　　

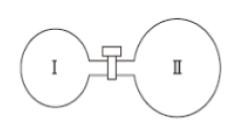
図のように断熱容器Ⅰ、Ⅱがコックが付いた細管で連結されている。

Ⅱの容積はⅠの容積の2倍でありコックを開いた状態で、これらの容器にある理想気体を封入したところ、温度が300K、圧力が1．00×10⁵Paとなった。

コックを閉じて容器Ⅱの気体のみを加熱し温度を480Kにした後、加熱を止め、コックを開いた。

平衡状態となったときの容器内の圧力はおよそいくらか。

ただし、容器の熱膨張、容器をつなぐ細管の容積は無視できるものとし、細管及びコックと封入した気体との熱のやりとりはないものとする。

1．1.5×10⁵Pa

2．1.4×10⁵Pa

3．1.3×10⁵Pa

4．1.2×10⁵Pa

5．1.1×10⁵Pa

 

 

 

 

 

　解 説　　　　　

理想気体というキーワードがあるのでPV = nRT を思い出します。

本問は「温度の違う気体をコックで分離しておき、コックを開いて混ぜた時の圧力を求める」という状況が特殊です。

状態方程式だけでは「コックを開いた時にT も P も変化してしまいわけがわからない」という問題があります。

そこで、理想気体に関するもう１つの重要な基礎知識である、気体の内部エネルギーに関する「U = 3/2 nRT」 を思い出して考えます。

※この式は単原子分子についての式ですが特に指定がないので単原子分子と仮定して考えます。

Ⅰの容積を V_容器 とします。Ⅱの容積は 2V_容器 です。

初めの状態において、圧力は 1, 体積は 3V_容器 なので PV = 1×3V_容器 です。

※ p について「× 10⁵」は略して考えます。選択肢を見ると係数だけわかれば答えが選べるからです。

理想気体の状態方程式（PV=nRT）より、nRT = 3V_容器 と表すことができます。

これを内部エネルギーの式（U = 3/2 nRT）に代入すれば

U = 3/2 × (3V_容器)
= 9/2 V_容器
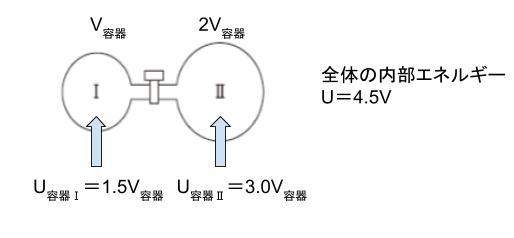
=4.5V_容器 です。

気体はまんべんなく存在するのだから、容器Ⅰと容器Ⅱの体積比が１：２であれば、気体の分布する比も１：２です。

つまり、容器Ⅰの気体の内部エネルギーと容器Ⅱの気体の内部エネルギーの比も１：２と考えられます。

従って、容器Ⅰの気体の内部エネルギーは 1.5V_容器、容器Ⅱの気体の内部エネルギーは 3V_容器と考えられます。

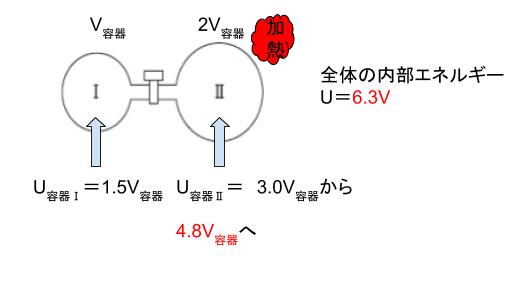
次に容器Ⅱだけ加熱されて 300K → 480K になりました。T が 1.6 倍なので内部エネルギーも 1.6 倍になります。3 × 1.6 = 4.8です。4.8V_容器 になります。

この状態でコックを開けば、全気体の内部エネルギーは 4.8V_容器 + 1.5V_容器 = 6.3V_容器 です。

すると、U = 3/2 nRT かつ、 nRT = PV なので、U が 6.3V_容器であればPV が 4.2V_容器 とわかります。

コックを開いて全体に注目しているため、Vは 3V_容器 です。4.2 ÷ 3 = 1.4 なので、P = 1.4 です。

正解は 2 です。