問 題
図のように長さLの2本の糸に、質量がそれぞれ2m、mの小球A、Bを取り付け、それぞれを天井の点Oからつるし、鉛直線と角θ、2θをなすように支えている。
いま、小球A、Bを同時に静かに放すとき、小球A、Bを放してから小球A、Bが最初に衝突するまでの時間として、最も妥当なのはどれか。
ただし、小球A、Bは、同一平面上を運動するものとする。
また、θは十分に小さいものとし、重力加速度の大きさをgとする。
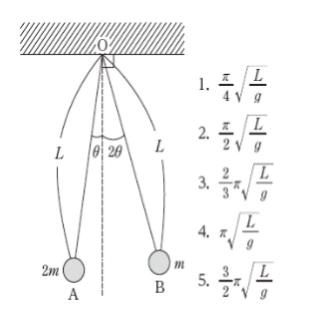
正解 (2)
解 説
単振り子なので周期の公式を思い出します。また2つの振り子を一気に考えることはできないので、1つずつ考えます。
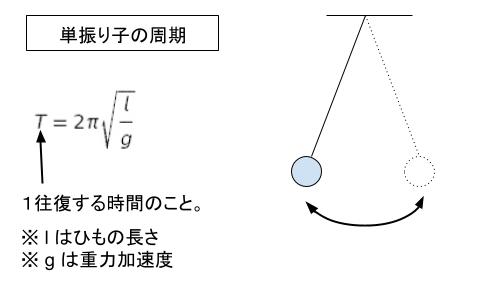
この公式から、ポイントはひもの長さだけで質量は関係ないということがわかります。そうすると球 A,B の周期は同じです。
従って、ちょうどど真ん中(Oのちょうど真下)で2つの球はぶつかるとわかります。その時間は「1往復が 1周期」なので、1/4 周期です。
よって、π/2 √L/g です。
正解は 2 です。

コメント