問 題
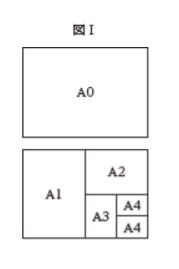
「A0」から始まるA版のサイズの用紙は,全て,短辺:長辺が 1: √2 の長方形であり,「A0」サイズの用紙の長辺の方を半分に折ると「A1」になり,同様に「A1」を半分に折ると「A2」となり,数字が一つ増すごとにその半分の寸法になる。この関係を示すと図Ⅰのとおりである。
いま,赤,黄,緑,青の各色の「A0」サイズの用紙が1 枚ずつあり,この 4 枚をそれぞれ,図Ⅰのように「A1」,「A2」,「A3」各1 枚と「A4」2 枚の計5 枚の用紙に切った。
これを図Ⅱのように,「A0」用紙4 枚分に相当する台紙の上に配置することとし,まず赤の5 枚の用紙(網掛け部分)を配置した。さらに,四隅については,赤の「A2」以外に,黄の「A1」,緑の「A3」,青の「A4」を配置した。
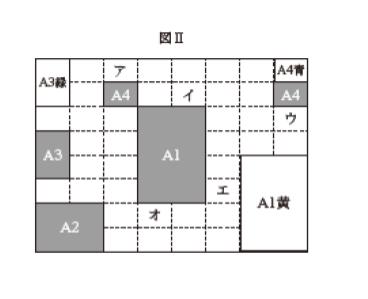
ここで,残った用紙を全て,次のように配置したとき,図Ⅱの台紙のア~オの場所のうち,青の用紙で覆われるもののみを挙げているのはどれか。
○ 台紙から用紙がはみ出したり,用紙どうしが重ならないようにする。
○ 同じ色の用紙と辺で接しないようにする。
○ 5 枚の赤の用紙は全て,黄,緑,青のどの色の用紙ともどこかの辺で接するようにする。
1.ア,ウ
2.ア,オ
3.イ,エ
4.イ,オ
5.ウ,エ
解 説
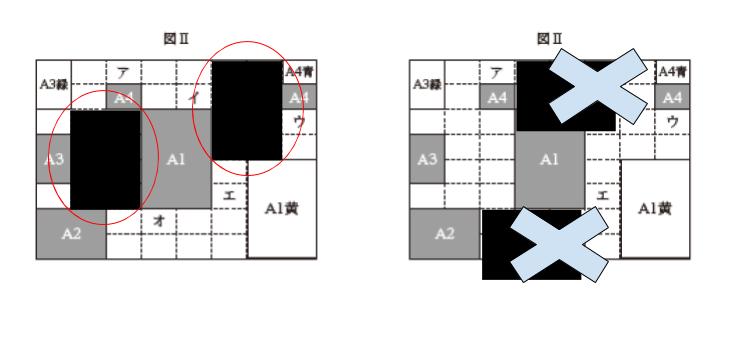
自由度が高すぎるように思えるのですが、そういう時は「厳しい条件、でっかいものから考える」です。残りの A1 2枚について考えると、2箇所しか入りません。下図参照。
※ 横向きを考えた人がいるのではないかと思いますが、はみでちゃいます!
右上の A1 は、右上隅に A4 青がいるから、青はだめです。よって、右上が A1 緑、左側の A1 が 青と確定します。本番では色とかつけれないから「A1緑、A1青」とか書いて考えるしかないと思います。
すると、ウは黄色じゃなきゃいけないので、ウが含まれる選択肢 1,5 は誤りとわかります。
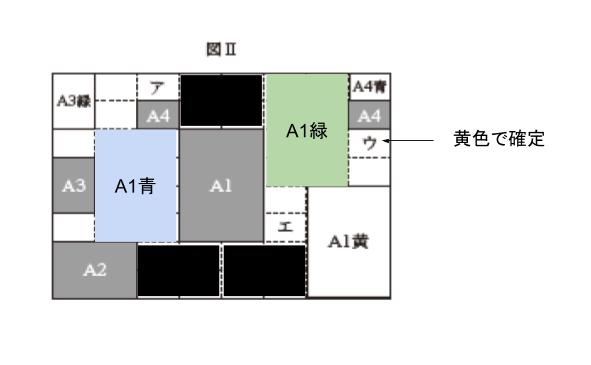
上図で黒く示した部分が A2 が入りうる部分です。従って、オ の所は青は絶対きません。選択肢 2,4 は誤りです。以上より、正解は 3 です。

コメント