問 題
新古典派成長モデルの枠組みで考える。ある経済のマクロ生産関数が,Yt = AKtα Lt1-α で与えられているとする。ただし,Yt ,Kt ,Lt は,それぞれ t 期における産出量,資本ストック,労働人口であり,A と α は定数である。
ここで,労働人口は時間を通じて一定で,Lt+1 = Lt ≡ L であるとする。
一方,t 期の粗投資を It ,資本減耗率を d としたとき,資本ストックの大きさは,投資によって,Kt+1 = Kt -d Kt + It で増加するものとする。また,各期における財市場は均衡しており,貯蓄率を s とおくと,It = s Yt である。
いま,生産関数の係数 A = 0.8,a =1/3 ,資本減耗率 d =0.04,貯蓄率 s =0.2 であるとする。
このとき,資本・労働比率(Kt /Lt)は,時間の経過とともにいくらに収束するか。ただし,初期
の資本ストックと労働人口は共に正の値であるとする。
1. 1
2. 8
3. 27
4. 64
5. 125
解 説
新古典派成長モデルということなので、ソロースワンモデルを考えます。成長率 ΔK/K = sy/k ー d・・・(1) です。ここで s は貯蓄率、y が 1 人あたり生産(Y/L)、k が 1 人あたり資本(K/L)です。H26 no40 と比較した際に、資本減耗率 d =0.04 がある点に注意が必要です。
定常状態において、ΔK/K = 0 です。従って、d = sy/k が成立します。d = 0.04,s = 0.2 を代入すれば、0.04 = 0.2 × y/k です。すなわち、0.04 = 0.2 × (Y/L)/(K/L)・・・(1) と表すことができます。
以下、添字の t を省略します。
問題文より、Y = AKα L1-α です。A = 0.8 です。α = 1/3 を代入した上で、両辺を L で割ります。すると、Y/L = 0.8 × (K/L)1/3 となります。 これにより、K/L についての式を、以下のように計算できます。
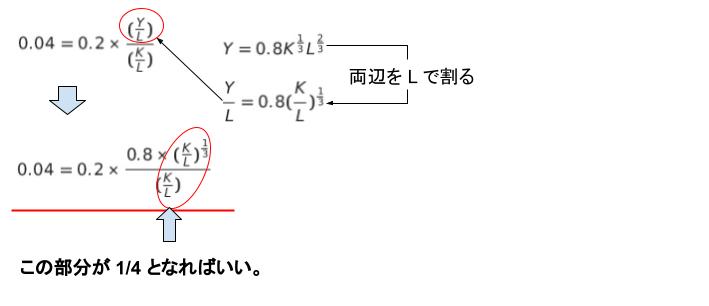
等号成立のためには、赤丸で囲んだ部分が 1/4 となればよいです。K/L の値として、選択肢の値を代入していけば、K/L = 8 の時、赤丸で囲った部分が 2/8 = 1/4 となります。
以上より、正解は 2 です。
類題 H26no40

コメント