公務員試験 H28年 国家一般職(行政) No.35解説

　問 題　　　　　

ある財の市場は，先に生産量を決定するリーダーの企業Ａと，それを受けて生産量を決定するフォロワーの企業Ｂの二社による寡占市場となっている。

この市場における逆需要関数は，P = 380 – 3（X_A + X_B）であるとする。ここで，P は財の価格，X_A は企業Ａの生産量，X_B は企業Ｂの生産量を表す。また，二企業とも費用関数は，C_i = 20 X_i + 50 であるとする。ここで，C_i は，企業 i（i = A，B）の総費用，X_i は，企業 i（i = A，B）の生産量を表す。このとき，シュタッケルベルク均衡における企業Ａの生産量はいくらか。

1． 30
2． 40
3． 45
4． 60
5． 90

 

 

 

 

 

　解 説　　　　　

複占における、フォロワーがいる場合のシュタッケベルク均衡についてです。仮定として「フォロワー側が、相手方の生産量を一定と考える」という点が基礎知識です。

企業 B の売上は、PX_B  = (380 – 3X_A – 3X_B) X_B  =  380X_B   -3X_A X_B   -3X_B ² です。費用が 20X_B   + 50 です。従って、利潤は 380 X_B   -3X_A X_B   -3X_B ² ー(20X_B   + 50) = 360X_B   -3X_A X_B   -3X_B ² – 50 です。

X_A を定数と考えます。X_B で微分して、= 0 となる式を反応関数といいます。反応関数は -6X_B  + 360 – 3X_A = 0 ・・・（１）です。

次に、 企業 A の利潤を考えます。
企業 A の売上は、PX_A = (380 – 3X_A – 3X_B) X_A = です。（１）より、X_B を消去して整理すると、以下のようになります。

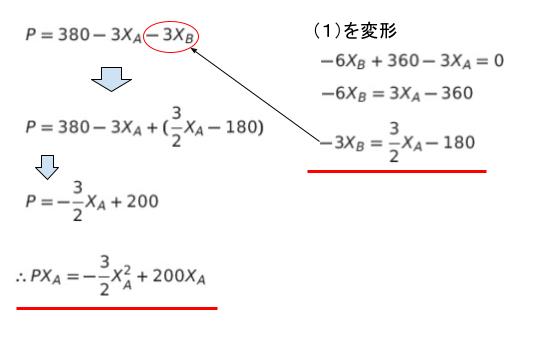
リーダーなので、利潤最大化条件が「限界収入＝限界費用」であることに注意します。限界収入は、先程もとめた PX = -3X_A ²/2 + 200 X_A を微分して、-3X_A + 200 ・・・（２）です。費用が 20 X_A  + 50 です。限界費用は、費用関数を微分すればよいので、２０・・・（３）です。（２）＝（３）が利潤最大化条件なので、-3X_A + 200 = 20 を解くと、X_A = 60 です。

以上より、正解は 4 です。