問 題
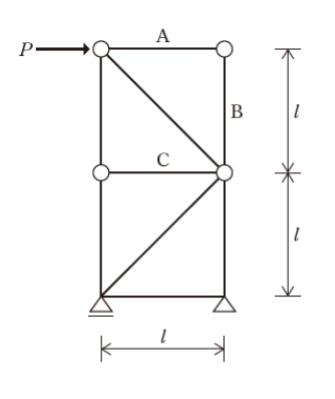
図のような荷重を受ける構造物の部材に生ずる軸方向力に関する記述㋐、㋑、㋒のうち妥当なもののみを全て挙げているのはどれか。ただし、縦方向部材は鉛直、横方向部材は水平であるとする。
㋐ 横方向部材 A の軸方向力の大きさは 0(ゼロ)である。
㋑ 縦方向部材 B の軸方向力の大きさは 0(ゼロ)である。
㋒ 横方向部材 C の軸方向力の大きさは 0(ゼロ)である。
1.㋐
2.㋐、㋑、㋒
3.㋐、㋒
4.㋑
5.㋑、㋒
解 説
【支点反力の計算】
まずは反力を求めます。右側の支点を A とおきます。A における垂直反力を RA、水平反力を HA、左側のローラー付き支点を B とおきます。B における垂直反力を RB とおきます。
横方向の力に注目すれば HA は、左向きに P です。
縦方向に注目すれば、RA + RB = 0 です。
A 点におけるモーメントを考えると
左上部分の「右向き P」の力によって、P × 2l (時計回り)のモーメントが生じます。
モーメントの和が0なので、RB = 2P とわかります。モーメントが反時計回りでないといけないので、力の向きは下向きです。
RA + RB = 0 より、RA = 2P です。向きは上向きです。
まとめると、以下のようになります。
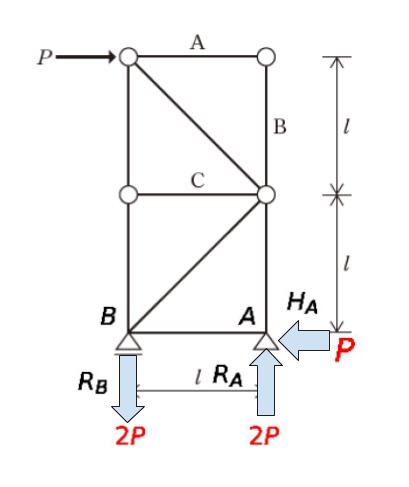
【接点法による軸力の計算】
軸力を「節点法」で考えます。
A から考えます。

AB 間の部材の軸力が 「←→」とわかるので
点 B において接点法で考えると、斜めの部材の軸力は↗です。これをふまえて各軸力を求めると以下のようになります。

左真ん中の接点に注目します。部材 C しか横方向の力を与えるものがありません。横方向の力の和が 0 なので、C の軸力は 0 とわかります。正解は 2,3,5 のどれかです。
C は部材0なので、以下、取っ払って考えます。
右側真ん中の接点に注目します。
横方向の力の和が0なので、↖方向の部材において軸力は↘ となります。すると斜めの軸材による縦方向の力が 2P(下向き)となります。縦方向の力の和が0なので、部材 B の軸力は0とわかります。正解は 2 or 5 です。

右上の点で接点法で考えれば、横方向の力の和が 0 より、部材 A の軸力が 0 は明らかとなります。
妥当なものは ㋐、㋑、㋒の全てです。
以上より、正解は 2 です。
類題 H27no83

コメント