問 題
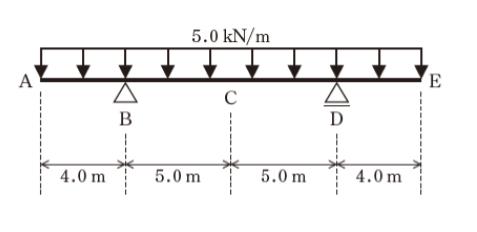
図のような張り出し梁に等分布荷重が作用している。この梁において、せん断力及び曲げモーメントが共にゼロとなる位置として妥当なもののみを全て挙げているのはどれか。
1.A
2.A、E
3.B、C、D
4.B、D
5.C
解 説
対称性に注目します。きれいに左右対称です。よって、例えば点 A でせん断力、曲げモーメントが0なら、E も全く同様に0になるはずと考えられます。これにより、選択肢 1 は誤りです。
点 A に注目し、せん断力、曲げモーメントについて考えます。
そのために、まずは反力を求めます。等分部荷重は集中荷重になおします。 18 m にわたり、5.0kN/m なので 18 × 5.0 = 90kN です。それを B,D で支えているため、反力はそれぞれ 45kN と考えられます。
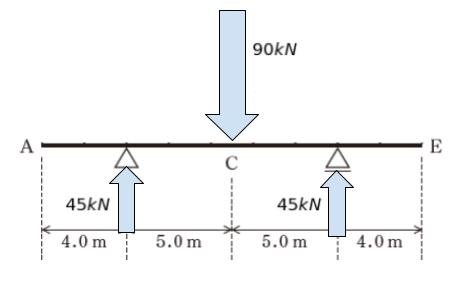
次に
「点 A におけるせん断力」、すなわち上下方向の力についてまず考えます。各点におけるせん断力やモーメントを考える時は、等分部荷重のままで考えて、考える点において仮想切断する点に注意が必要です。(点 A や点 E は端点なので、等分部荷重を集中荷重になおした時に、上図と同じになります。従って、点 A のせん断力、モーメントを考える時は、上図で考えればよいです。)
反力と集中荷重で、足して0なので、上下方向の力は点 A にはかかっていません。つまり、点 A におけるせん断力は 0 です。
そして
「点 A まわりのモーメント」を考えます。反力により、反時計回りにそれぞれ 45 × 4.0 = 180、45 × 14 = 630、合わせて 810 のモーメントが生じます。集中荷重により、時計回りに 90 × 9 = 810 のモーメントが生じます。これで足して 0 なので、点 A にモーメントはかかっていません。点 A の曲げモーメントは 0 です。
対称性より、E も同様です。これにより、A,E が妥当とわかります。
以上より、正解は 2 です。

コメント