公務員試験 H28年 国家一般職(土木) No.2解説

　問 題　　　　　

図において線分 AR,RC の長さはそれぞれ 3,2 である。また、線分 AQ は△ABC の頂点 A における外角の二等分線であり、線分 PC と線分 AQ は平行である。

このとき、線分 AB の長さはいくらか。

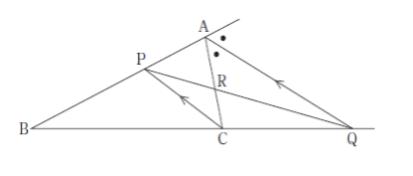
1. 7
2. 8
3. 10
4. 12
5. 15

 

 

 

 

 

　解 説　　　　　

※外角の二等分線の公式は不要。

△CPRと△AQR がいわゆるちょうちょの関係で相似。相似比２：３。したがって、PC：QA も２：３。

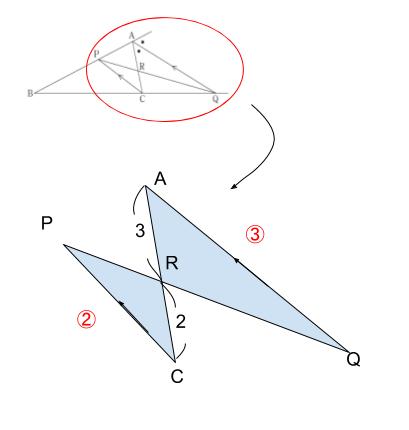
ここで図が明らかに変なんだけど、△APCに注目するとAP=ACの二等辺三角形となる。理由は下図の通り。

※青い○と赤い○は同じ角度

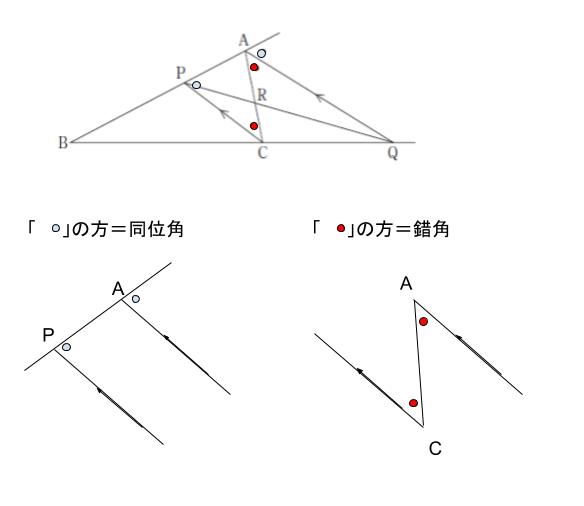
つまりAP = AC = 5。

最後に△BPCと△BAQ のいわゆるとんがり帽子の相似に注目すれば、PC：QA = 2：３より、BP：BA が２：３。ということは、BP：AP = 2：１とわかる。

APの長さは５とわかっているのでBPの長さが１０。ABの長さは AP＋PB なので５＋１０で、答えは１５。

正解は 5 です。