問 題
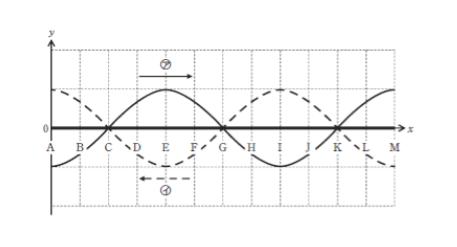
振幅と波長がそれぞれ等しい二つの波 ㋐(実線) 、㋑(破線)が互いに逆向きに進んでおり,図は時刻 t = 0 [秒] のときの二つの波の様子を表している。このとき二つの波の合成波は x 軸と一致する。
波の周期は両方とも8秒であるとすると時刻 t = 2 [秒] のとき、二つの波の合成波において y = 0となる点は、A~Mのうちに何点あるか。ただし二つの波は無限に続いており振幅は減衰しないものとする。
1. 1点
2. 2点
3. 4点
4. 6点
5. 8点
正解 (3)
解 説
波が出てきたので、波の基本式を思い出しておきます。 v = fλ です。
本問では λ は 8マスです。T = 1/f なので、T = 8 なら、f = 1/8 です。
従って、v = 1/8 × 8 = 1 マス/秒 です。
(こんな計算しなくても、なんとなく周期8で、ちょうど8マスで1波だから、1秒で1マスと考えてもなんとかなります。)
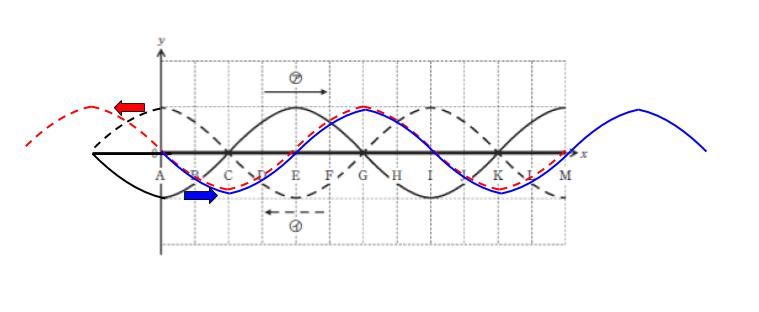
それぞれの波の 2 秒後を考えます。以下のようになります。青い実線が 2 秒後の㋐、赤い点線が 2 秒後の㋑です。重なります。よって、合成波において y = 0 となるのは、波の y = 0 のところです。つまり A,E,I,M の 4 点です。
以上より、正解は 3 です。

コメント