問 題
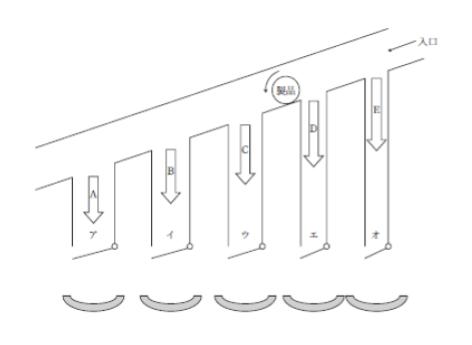
ある工場ではA~Eの5種類の製品を製造しており、製品1個当たりの重さは、製品Aが100g 製品Bが50g 製品Cが10g 製品Dが5g 製品Eが1g である。この工場にはこれらの製品を仕分ける図のような装置がある。
この装置に入口から製品を入れると、製品Aはアのみに、製品Bはイのみに、製品Cはウのみに、製品Dはエのみに、製品Eはオのみにそれぞれ入るようになっている。
アは製品Aが1個入ると底が開いて製品が下の受け皿に落ち再び底が閉じて製品Aが入るようになっている。またイ~オはそれぞれ製品Bが2個製品Cが3個製品Dが4個製品Eが5個たまると底が開いて製品が下の受け皿に落ちて空になり再び底が閉じて各製品が入るようになっている。
いまこの装置に製品が一つも入っていないことを確認した上で9個の製品を入口から順に入れたところ合計3回底が開いてア~オのいずれにもたまっている製品はなかった。
このときこれら9個の製品の組合せとして考えられるもののうち重さの合計が最も重い組合せと最も軽い組合せの重さの差はいくらか。
1. 55g
2. 70g
3. 85g
4. 100g
5. 115g
解 説
重さ最大にしようと思って、A1個、B2個と入れてしまうと、製品を9個入れてきれいに全て落とすことができなくなります。そこで、B4個(2個で下に1回落ちる)、E5個の組み合わせが一番重いとわかります。これで 205g です。
一方、重さを最小にしようと E を 1 回使ってしまうと、残製品 4 個で、2回底に落とさなければいけないので、どうしても A 1回や、B1回が必要なので 100g を超えてしまいます。
Dを1回使っても、やはり残製品5個、2回底に落とさなければならないので、どうしてもB1回必要なので、100g を超えます。そこでC9個とすると、3回×3で 90g が最小とわかります。
205ー90 = 115g です。正解は 5 です。

コメント