問 題
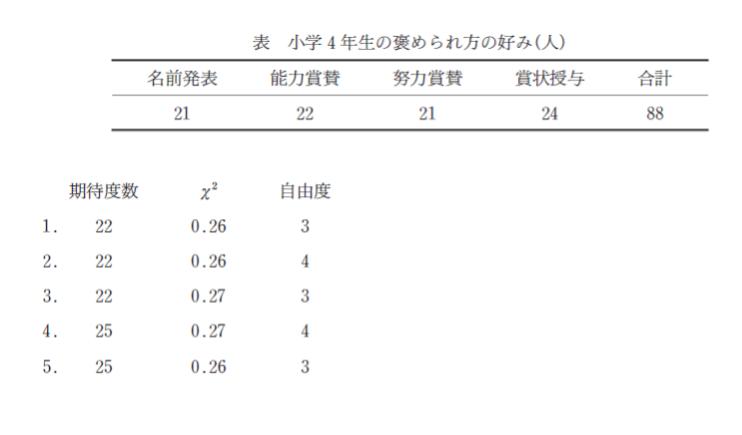
小学4年生88人を対象に先生に褒められるとしたらどんな褒められ方を好むかを四つの選択肢 (名前発表・能力賞賛・努力賞賛・賞状授与) の中から選ばせたところ1×4の集計表が得られた (下表) 。この結果から特に小学4年生の好む褒められ方があるといえるかどうかを検討するために褒められ方の好みに差はないと仮定し χ2 検定を行うことにした。期待度数 χ2 自由度の値の組合せとして最も妥当なのはどれか。
解 説
χ2 値は『Σ(観測値ー理論値)/理論値』です。本問では、褒められ方の好みに差がなければ、どれも 22 になるはずです。従って、理論値は 22 です。
χ2 = {(21-22)2 + (22-22)2 + (21-22)2 + (24-22)2}/22
= 6/22 = 3/11 ≒ 0.27 です。また、期待度数が 22 なので、正解は 3 です。
ちなみにですが
自由度とは、変数のうち一つを固定した時に自由に決めることができる残りの変数のことです。本問でいう変数とは、4 つの選択肢の数値です。合計が 88 と決まっているので、1つ数値が決まれば、残り3つを自由に(和が 88 の範囲で)選ぶことができます。4-1 = 3 です。
自由度に関して、「行の数-1」×「列の数-1」とおぼえている人もいるかもしれません。その場合、本問では「0×3で 0」と考えて困ったのではないでしょうか。
χ2 検定では、理論値とのずれを考えているので、ある意味でこの表はもう一行「22,22,22,22」という理想の数値の行が隠れており、その2つの行に注目して適合度を検定しているといえます。1×4に見える表を「2×4」の表とみなせば「(2-1) × (4-1) = 1 × 3 = 3」となります。

コメント