公務員試験 H27年 国家一般職(土木) No.26解説

　問 題　　　　　

図のような円形断面のパイプ中を水が流れている。

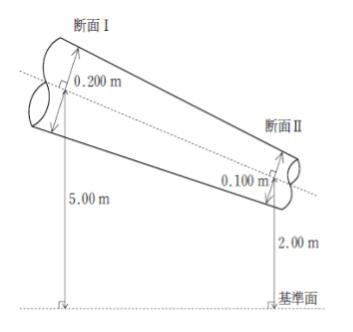
水平な基準面から5.00mの高さに位置する断面Ⅰの内径は0.200m、基準面から2.00mの高さに位置する断面Ⅱの内径は0.100mであり、断面Ⅰにおける圧力は30.0kPa、流速は1.00m/sである。

このとき、断面Ⅱにおける圧力はおよそいくらか。

ただし、水の密度は1.00×10³kg/m³、重力加速度の大きさは10.0m/s²とし、パイプ内のエネルギー損失は無視する。

1. 42.5kPa
2. 52.5kPa
3. 62.5kPa
4. 72.5kPa
5. 82.5kPa

 

 

 

 

 

　解 説　　　　　

ベルヌーイの定理より

v₁²/2g + z₁ + p₁/ρg = v₂²/2g + z₂ + p₂/ρg

また、連続の式

Q=AV

です。

内径の比が２：１であれば面積の比は４：１となります。流量は一定だから、連続の式より速度の比が１：４とわかります。

断面Ⅰの流速が 1m/s なので断面Ⅱの流速は 4m/s です。

以上より、p₂ 以外の変数の値が全てわかったので代入してみると

1²/2・10＋５＋30/1・10  = 4²/2・10+2+p₂/1・10
↔1/20 + 8 = 16/20 + 2 + p2/10
↔p₂/10 = 6ー15/20
↔p₂ = 60ー7.5 （両辺に 10 をかけました。）

よって、p₂ = 52.5 となり

正解は 2 です。