問 題
三角関数に関する次の記述の㋐、㋑に当てはまるものの組合せとして最も妥当なのはどれか。
「三角関数の加法定理よりsin(α+β)=( ㋐ )が成り立つ。これを用いると、cos45°sin75°=( ㋑ )と計算できる。」

解 説
㋐は公式ですが、覚えていなかったとしても選択肢からぜひ判断してほしい所です。
選択肢を見れば答えの候補は「sinαsinβ ー cosαcosβ」と「sinαcosβ+cosαsinβ」の2つです。
sin30°や60°の値ならわかるはずなので、α = β = 30°として検討します。
α = β = 30°であればα+β = 60°です。sin 60° = √3/2 です。
一方、sin30°sin30°ーcos30°cos30°は
(1/2)2ー(√3/2)2
=1/4 ー3/4
=ー1/2
です。一致しません。sin(α+β)≠sinαsinβ ー cosαcosβ です。
従って、sin(α+β) = sinαcosβ+cosαsinβ です。
正解は 3~5 とわかります。
次に、cos45°sin75°を考えます。
cos45°は√2/2 です。sin75°を、先程の公式で計算しなさいという問題です。sin75°=sin(45°+30°)として公式に代入します。
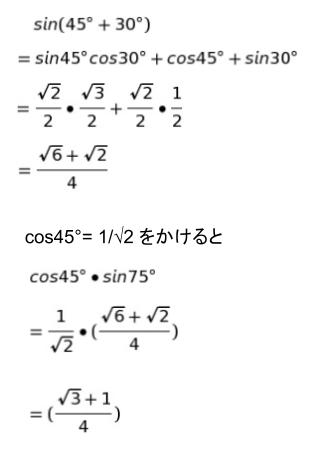
となります。
正解は 5 です。
ちなみにですが、sin75°は、公式を使わず選択肢の大雑把な評価でも解けます。
√2 ≒ 1.41、√3 ≒ 1.73 です。よって、選択肢 3~5 の答えはそれぞれ以下のように評価できます。

cos45°=√2/2 なので、cos45°≒ 1.41/2 ≒ 0.7 です。
sin75°はsin60°=√3/2 より明らかに大きいです。√3/2 ≒ 1.73/2 ≒ 0.86 です。
cos45°×sin60°が大体 0.7× 0.86 = 0.62 なので、cos45°×sin75°は0.62よりも大きいはずです。
従って、選択肢 3,4 では値が小さすぎます。
よって、正解は 5 です。

コメント