公務員試験 H27年国家一般職(電気・電子・情報) No.26解説

　問題　　　　　

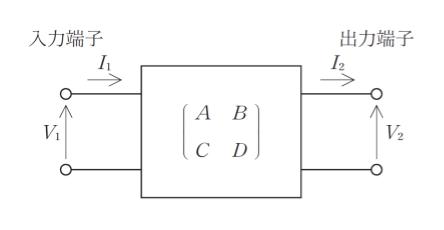
四端子回路に関する以下の記述の㋐～㋓に当てはまるものの組合せとして最も妥当なのはどれか。

「図のような四端子回路において電圧 V₁,V₂ 及び電流 I₁,I₂ を図の向きにとったとき縦続行列は

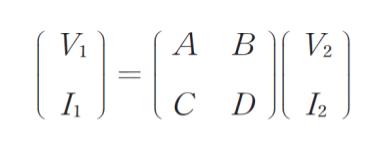
で定義される。

縦続行列の各要素の物理的意義を考えると A は出力端子を開放したときの㋐との比であり、D は出力端子を短絡したときの㋑との比である。同様に B は出力端子を短絡したときの V₁ と I₂ との比であり C は出力端子を開放したときの I₁ と V₁ との比である。したがって B は㋒の次元をもち C は㋓の次元をもつ。」

	㋐	㋑	㋒	㋓
1.	V₁ と I₂	I₁ と V₂	アドミタンス	インピーダンス
2.	V₁ と I₂	I₁ と V₂	インピーダンス	アドミタンス
3.	I₁ と V₂	V₁ と I₂	インピーダンス	アドミタンス
4.	V₁ と V₂	I₁ と I₂	アドミタンス	インピーダンス
5.	V₁ と V₂	I₁ と I₂	インピーダンス	アドミタンス

正解 (5)

　解説　　　　　

H25no26 を参考に、右辺の行列を計算すれば「V₁ = AV₂ + BI_2」、「I₁ = CV₂ + DI_2」です。A~Dを解くために、四端子行列でできることは、出力端子をつなげて（短絡して） V を 0 にする　か、出力端子を解放して I = 0 にする　です。※入力の V や I を 0 にしちゃうと、この回路に何も流れず意味がない。そのため出力側をいじります。出力端子解放 → I₂ = 0 なので、式（１）より A = V₁/V₂ です。よって正解は 4 or 5 です。

次に問題文より、B は V₁ と I₂ の比、つまり V₁/I₂ です。※ 式（１）において、出力端子を短絡し V₂ = 0 を代入すれば導けます。この次元がインピーダンスかどうかという問題です。インピーダンスとは一般化した抵抗です。一方、オームの法則 V = RI より、R = V/I です。よって、V/I の形であれば、抵抗であろうと判断できます。従って、B の次元がインピーダンスと考えられます。

以上より、正解は 5 です。
類題 H25no26

コメント