公務員試験 H27年 国家一般職(電気・電子・情報) No.23解説

　問 題　　　　　

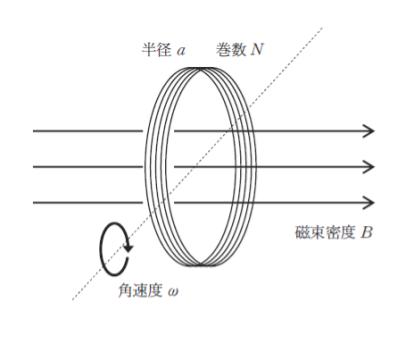
図のように磁束密度 B の一様な磁界の中で、半径 a、巻数 N の円形コイルが、磁界の方向と直角な直径を回転軸として角速度 ω で回転している。このコイルに発生する誘導起電力の最大値を４倍にする方法として記述 ㋐ ～ ㋔ のうちから妥当なもののみを全て挙げているのはどれか。

㋐ 半径 a を２倍にする。
㋑ 半径 a を４倍にする。
㋒ 巻数 N を２倍にする。
㋓ 巻数 N を４倍にする。
㋔ 角速度 ω を２倍にする。

1. ㋐ ㋒ ㋔
2. ㋐ ㋓
3. ㋑ ㋒
4. ㋑ ㋓
5. ㋔

 

 

 

 

 

　解 説　　　　　

類題 H24no23 より、ファラデーの電磁誘導の法則、V = -N(dΦ/dt) です。Φは磁束です。磁束が 4 倍になるには、磁力線が貫く面積が４倍になればよいので、円の面積が４倍になればよいです。そのためには、「半径を 2 倍」にすればよいです。また、N を 4 倍にしても、V が４倍になります。

以上より、正解は 2 です。