問 題
ある科目について試験を実施し成績を決めることとした。試験の実施方法及び成績の決定方法は次のとおりである。
<試験の実施方法>
初めにA B Cの3分野について各分野別に学生全員に試験を実施し分野別に合格又は不合格の判定を行う。3分野全てで不合格とされた学生を除いた残りの学生を対象にDの分野の試験を実施する。
<成績の決定方法>
4分野全てで合格した者:「優」
合格した分野数が3であった者:「良」
合格した分野数が2であった者:「可」
合格した分野数が1又は0であった者:「不可」
A B Cの3分野の試験を終了した時点でその結果は次のとおりであった。
○ 分野Aの合格者は170人、分野Bの合格者は80人、分野Cの合格者は120人であった。
○ 3分野全てで合格した者は30人であった。
○ 合格した分野数が2であった者は120人であったが、B、Cの2分野のみの合格者はいなかった。
○ 合格した分野数が1であった者は40人であったがBの1分野のみの合格者はいなかった。
分野Dの試験を終了して成績等は次のとおりであった。
○ 「優」となった者は20人、「良」となった者は70人、「可」となった者は80人であった。
○ 分野Dの合格者は全員分野Cでも合格していた。
このとき確実にいえるのはどれか。
1. 分野Aで不合格とされ成績が「良」又は「可」であった者は50人である。
2. 分野Bで不合格とされ成績が「可」であった者は30人である。
3. 分野Cで合格した者のうち成績が「良」であった者は50人である。
4. 分野Dの試験の受験者の合格率は5割未満である。
5. 成績が「不可」であった者は少なくとも30人いる。
解 説
3つの試験について合格してたり不合格だったりなので、ベン図で考えます。
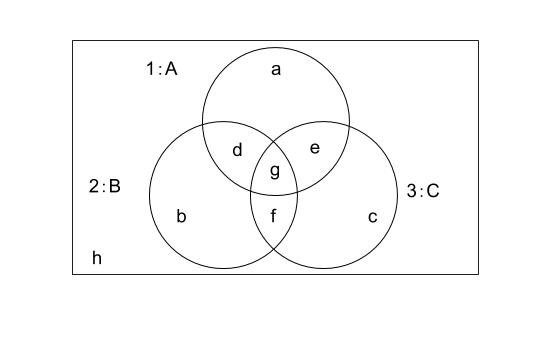
・「Aの合格者 170 人」→a+d+e+g = 170
・「Bの合格者 80 人」→b+d+f+g = 80
・「Cの合格者 120 人」→c+e+f+g = 120
・「3分野全てで合格した者は30人」→g = 30
・「B、Cの2分野のみの合格者はいなかった」→f = 0
・「合格した分野数が2であった者は120人」→d + e = 120
・「Bの1分野のみの合格者はいなかった」→b = 0
・「合格した分野数が1であった者は40人」→a + c = 40 です。
上から2番目の式に注目すれば、b = f = 0,g = 30 より、d = 50 です。
下から 3 番目の式より、d = 50 なら、e = 70 です。
上から 3 番目の式より、e = 70,f = 0,g = 30 だから、c = 20 です。
一番下の式より、a = 20 です。
アルファベット順にまとめると
a = 20,b = 0,c = 20,d = 50,e = 70, f = 0,g = 30 です。※ h は不明。
これをふまえ、選択肢を検討します。
選択肢 1 ですが、分野 A で不合格なので、b,c,f,h について考えます。h の人は D の試験を受けることができず、必ず不可です。b = f = 0 なので、c の 20 人だけ考えればOKです。この子たちは、D試験に合格しても、やっと可です。従って、明らかに誤りです。
選択肢 2 ですが、分野 B で不合格なので、a,c,e,h について考えます。h はみんな不可です。a = c = 20,e = 70 です。a の 20 人は、分野 C に不合格だから、Dでも不合格で、不可です。
残り c と e について検討します。g の 30 人のうち、20 人が優なので、10 人が良です。他に良となりえるのは、e の子だけなので、e の 70 人のうち 60 人が 良、10 人は可です。
ここで、d の子は、Dで不合格で可のはずです。これが 50 人です。可が全部で 80 人だから、あと 20 人が可です。可になりえるのは、残り c しかないので、 c の子がみんな D で合格で可だったと考えられます。すると、確かに分野 B で不合格 かつ 成績が可だった者は 30 人です。正解は 2 です。
選択肢 3 ですが、先程の考察から、分野 C で合格した者のうち、良は e から 60 人と、g から 10 人で、計 70 人です。
選択肢 4 ですが、c の 20 人と、e の 70 人中 60 人と、g の 30 人中 20 人が合格しており、明らかに 5 割以上です。
選択肢 5 ですが、不可は、a の 20 人しか確定しません。よって誤りです。
以上より、正解は 2 です。
類題)H24no16 (専門職 教養)

コメント