問 題
2個の重水素原子核が互いに等しい運動エネルギーで正面衝突して
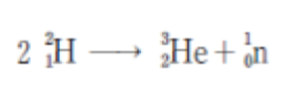
この核反応に関する次の記述の ㋐、㋑ に当てはまるものの組合せとして最も妥当なのはどれか。
ただし、重水素、He のそれぞれの原子核 及び 中性子の質量は、それぞれ
3.3436×10-27kg、5.0064×10-27kg、1.6749×10-27kgとし、真空中の光速度は3.0×108m/sとする。
また、この核反応では、エネルギーを運び去る光子などの粒子はなかったものとする。
・ この核反応で放出される核エネルギーはおよそ( ㋐ )×10-13 Jである。
・ 核反応後の He と n の運動エネルギーをそれぞれ K1、K2 とする。この衝突において運動量が保存されると仮定すると、K1:K2 はおよそ1:( ㋑ )である。
㋐ ㋑
1.2.7 1
2.2.7 2
3.2.7 3
4.5.3 2
5.5.3 3
解 説
E=mc2 を知っている前提です。
式の左辺における質量は、重水素が2つなので
3.3436×10-27kg × 2 です。
式の右辺における質量は、ヘリウム1つと中性子1つなので
5.0064×10-27kg + 1.6749×10-27kgです。
係数部分を計算してみると
6.6872 と、6.6813 です。わずかに減少しており、その差は
0.0059 = 5.9 × 10-3とわかります。
質量差分のエネルギーは、E = mc2 より
E = (5.9 × 10-3)×(3.0×108)2 ≒5.3 × 1013 です。よって正解は 4 or 5 です。
核反応の模式図を書くと、下図のようになります。
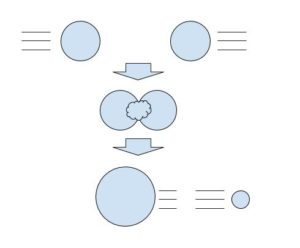
衝突は、同じ重水素が互いに等しい運動エネルギーだった ということなので、衝突における速度も同じだったとわかります。すると、衝突前において運動量は同じ大きさで逆向きなので、足せば0です。
衝突後において、Heの速度を ーv、中性子の速度を V とおきます。大雑把な比がわかればよいので、He の質量を5、中性子の質量を 1.67 とした上で、比で考えて 「3」:「1」とおきます。すると運動量は
3 ×(ーv)+1 × V と表すことができます。
衝突の前後で運動量が保存されたのだから
0=3×(ーv)+1×V です。従って、3v=V です。よって、v = 1/3 V と表すことができます。
He の運動エネルギーは
1/2 × 3 × (1/3V)2 = 1 / 6 V2 です。
中性子の運動エネルギーは
1/2 × 1 × V2 = 1/2 V2 です。
1/6:1/2 = 1:3 となります。
以上より、正解は 5 です。

コメント