問 題
図のように、密度 ρ [kg/m3] , 底面積 S [m2]、高さ h [m] の円柱が取り付けられた同じ軽いばねが二つ天井に取り付けられている。一方を液体に 3/4 h [m] だけ浸したところ、どちらのばねも静止し液体に浸した方のばねの伸びは、もう一方のばねの伸びの 1/2 倍であった。
このときこの液体の密度として最も妥当なのはどれか。ただし重力加速度の大きさは一定である。
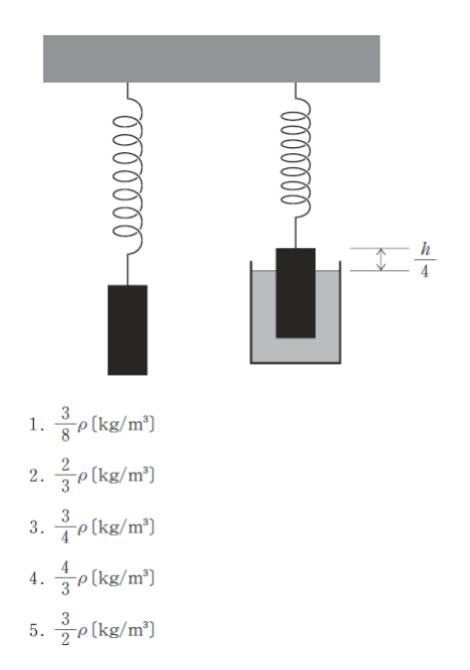
正解 (2)
解 説
V = Sh。m = Vρ です。これは基礎的知識です。
まず、図の左側のばねに注目します。質量 m [kg] の物体があれば、下向きに F = mg の力がかかります。ばねの伸びは、F = kx ∴ x = F/k で表されます。
次に、右のばねに注目します。同じばねなので k は同じです。伸びが半分ということは、F が半分ということです。液体に浸している方には、浮力がかかります。この浮力が ちょうど mg の半分、すなわち mg/2 であるとわかります。
浮力は公式です。F浮力 = ρ液体V排除された液体 g です。
排除された液体の体積が 3/4 V なので 、選択肢に注目すればρ液体が 2/3 ρ の時にちょうど
F浮力
=1/2 Vρg
= 1/2 mg
になります。(∵ Vρ = m)
以上より、正解は 2 です。

コメント