問 題
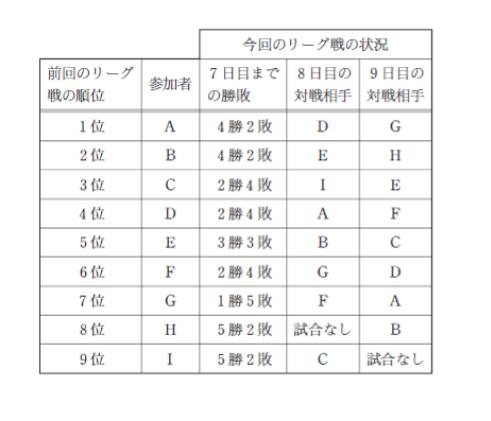
A~Iの9人が総当たりでバドミントン(シングルス)のリーグ戦を行った。このリーグ戦は9日間で行われ、各日とも試合がない者が1人いた。表は前回のリーグ戦の順位と、今回のリーグ戦の7日目までの各参加者の勝敗及び8日目と9日目の対戦相手を示したものである。
今回のリーグ戦では勝ち数が多い順に順位を付け、勝ち数が同じ者の順位については前回のリーグ戦の順位が高い者を上位とすることにしたところ、最終順位はAが1位、Bが2位、Cが5位、Dが最下位という結果となった。
今回のリーグ戦の勝敗や順位について確実にいえるのはどれか。ただし引き分けの試合はなかった。
- Aは6勝2敗であった。
- BはHに敗れた。
- Eは4勝4敗であった。
- Gは8日目と9日目のどちらかに敗れた。
- Iは3位であった。
解 説
D が最下位 になるためには、8日目、9日目に 1勝もできません。なぜなら、1勝してしまうと、3勝5敗になり、どうしても G よりも上の順位になってしまうからです。さらに、G は2勝しなければなりません。(Aに 9 日目で G は奇跡の勝利を上げる、ということが確定します!)
そうすると、Aは 8 日目の D には絶対に勝利しています。もしも D に負けてしまうと、G にも負けることになっているため、H や I が既に5勝しており、A が 1 位になれないからです。さらに、A が 5勝3敗で 1 位なので、H や I はもう1勝もしていません。
ここまでのわかった勝敗を表に書き込むと、以下のようになります。
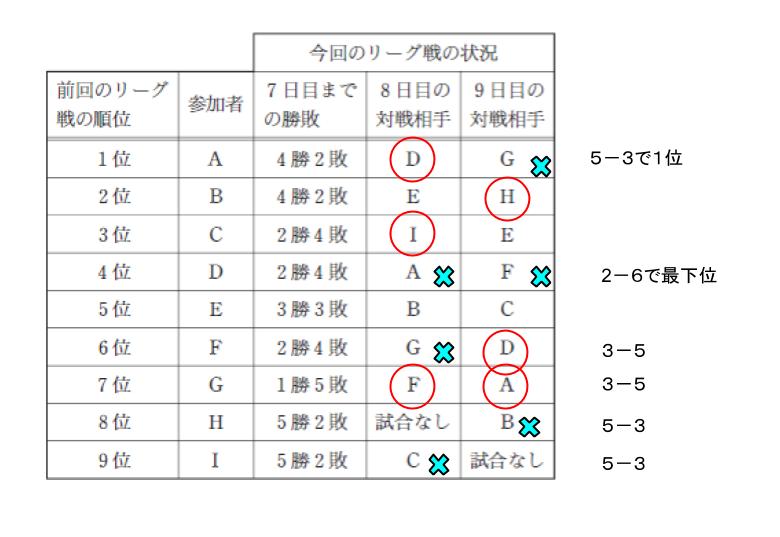
ここまでで、選択肢 1,2,4 は明らかに誤りです。さらに、 B が2位なので、 5勝3敗が最低でも4人いることなり、I は前回のリーグ戦で最下位なので、3位には絶対になれません。以上より、選択肢 5 も誤りです。正解は 3 です。
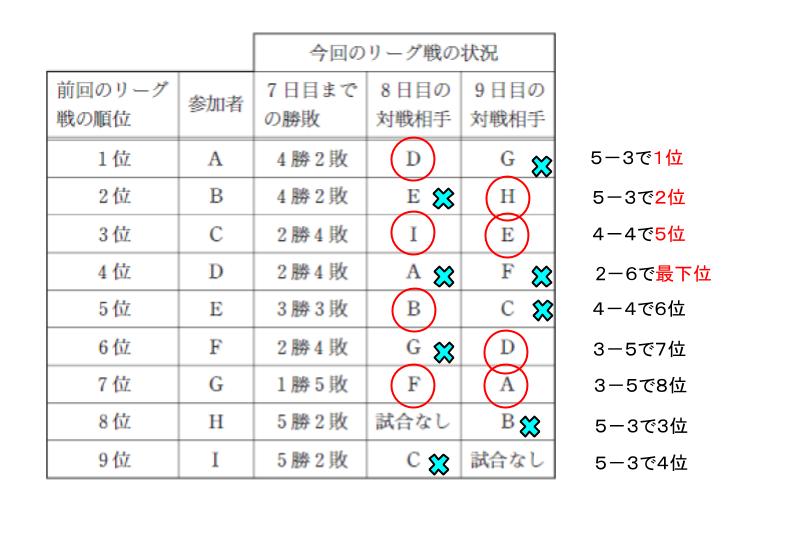
一応、残りを確定させるのであれば、 B が2位なので、B-EでEが勝っており、Cが5位にならなければいけないので、C は E に勝利する必要があります。従って、最終的に以下のように確定し、E は確かに 4 勝4敗です。

コメント