問 題
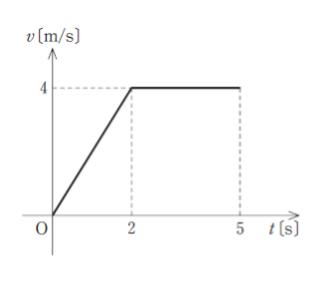
図は直線上を動く質量 2 kg の物体の時刻 t [s] (0≦ t ≦ 5) における速度 v[m/s] を表す。t = 0s から t = 5s までの間において物体に加えた力の大きさの最大値 F[N] と物体が移動した距離 L[m] の組合せとして最も妥当なのはどれか。
F L
1. 2N 12m
2. 4N 12m
3. 4N 16m
4. 8N 12m
5. 8N 16m
正解 (3)
解 説
グラフはいわゆる v-t グラフです。t = 0~2 では速度が増加していっており、しかも傾きが直線なので「等加速度運動」と考えられます。物理の重要な考え方は「速度が変わっている」ってことは「力が働いている」と読み替えるということです。
一方、t = 2~5では、速度は 4m/s で一定です。「等速直線運動」と考えられます。この時、力はかかっていません。
力の大きさの最大値ですが、そもそも力がかかっているのが t = 0~2 なので、この範囲に注目します。t = 0~2 において、2秒間で速度が 4 上がっています。従って、加速度 a は 2m/s2 です。
公式 F = ma より F = 2 × 2 = 4 です。これが力の最大値です。正解は 2 or 3 です。
距離については t = 2~5 に注目すれば、4m/s で 3 秒動けば 12m です。 12 よりは大きいので、選択肢 2 は誤りとわかります。ちなみに、v – t グラフでは、囲まれた部分の面積が距離を表します。面積を計算すれば 16 とわかります。
以上より、正解は 3 です。

コメント