問 題
定積分
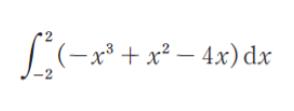
はいくらか。
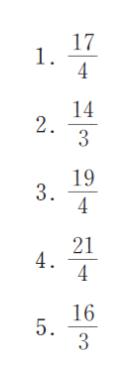
正解 (5)
解 説
まず、数字のついてない ∫ 式 dx を計算します。これは「微分したら式になるのはなんだ?」という計算と考えればよいです。∫ xn dx = xn+1/(n+1) が基本公式です。以下のようになります。

小さな数値の処理ですが、不定積分の結果(-x4/4 + x3/3 – 2x2) に対して「上の数値を代入ー下の数値を代入」すれば OK です。
x = 2 を代入すると -4 + 8/3 – 8 です。
x = -2 を代入すると -4 – 8/3 – 8 です。引き算すると 16/3 です。
以上より、正解は 5 です。

コメント