問 題
粗い水平面に置かれた幅D、高さH、奥行きB、質量Mで一様な直方体の図Ⅰに表す位置に水平な力F(θ)を加えて、図Ⅱのように直方体をゆっくりと傾けた。
このとき、直方体の底面と水平面のなす角θの関数であるF(θ)として最も妥当なのはどれか。
ただし、直方体と水平面との間で滑りは生じないものとする。また重力加速度の大きさをgとする。
なお、図は直方体がθ傾いたときの拡大図である。

解 説
図Ⅱ、Ⅲをちょっと立体的に書いて、中心を「O」、力がかかっている点を「B」と名付けたのが下図です。
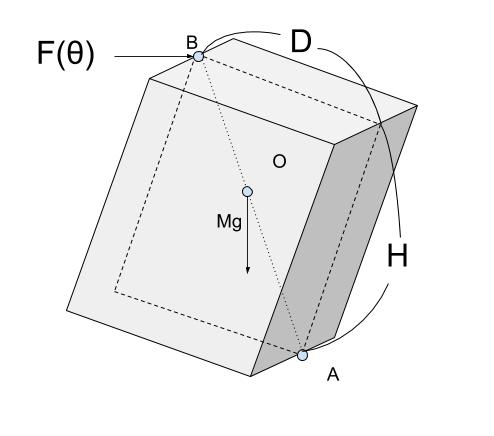
静止しているのでΣ縦=0、Σ横=0なのですが、そこからは F(θ) について何もわかりません。そこで、点A周りのモーメントを考えてみます。
力がかかっているのはAB上だけなので、線分ABを抜き出してみると以下の図のようになります。
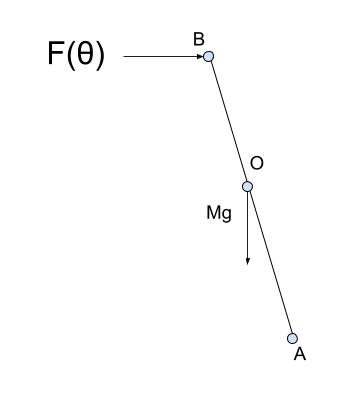
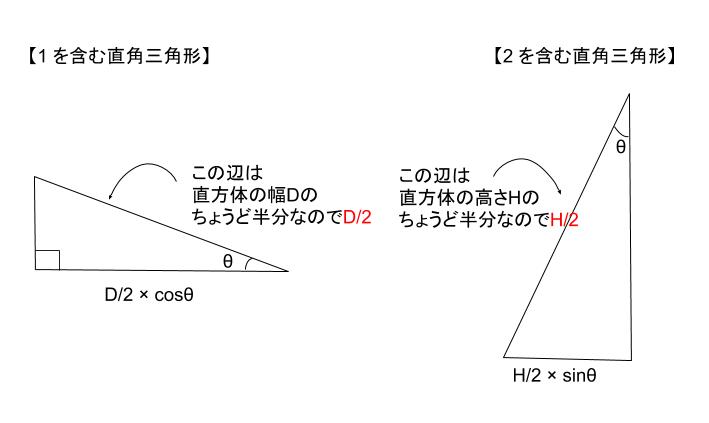
モーメントは、力×距離で求めます。まず、Mg の力 と 点Aの距離から考えます。下図の右側の図における赤い線の長さが「Mg の力 と 点Aの距離」です。
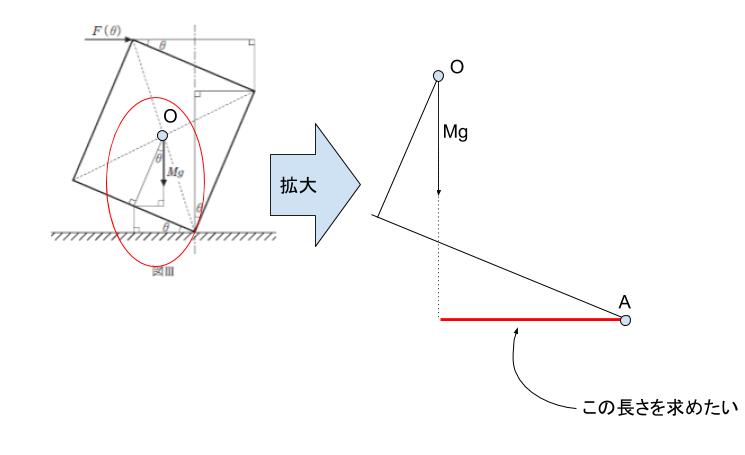
求めたい長さは、下図における赤い線「1」の長さから赤い線「2」の長さを引けばよいとわかります。
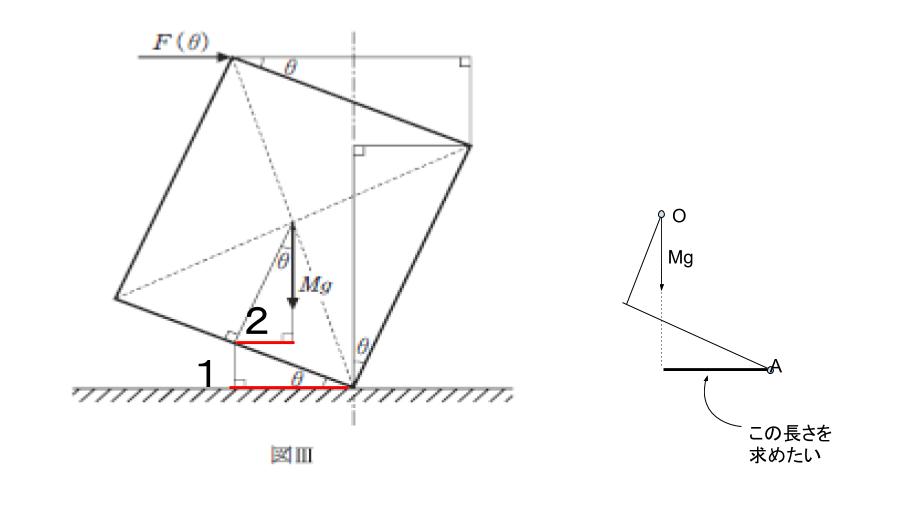
すると「1」及び「2」を含む直角三角形に着目すれば、1の長さは D/2 cosθ、2の長さは H/2 sinθ です。
以上より、Mg によるモーメントは、
Mg×(D/2 cosθーH/2 sinθ)・・・(1)です。
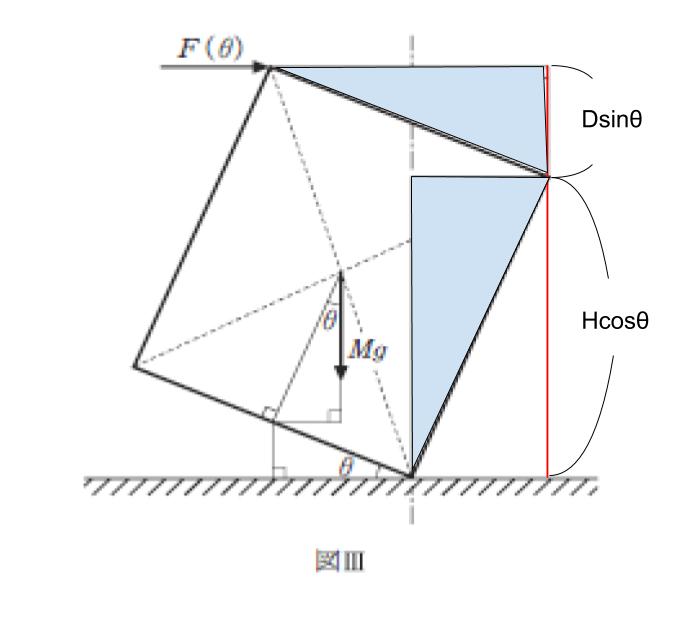
同様に、F(θ) によるモーメントも考えるために下図のように注目すれば、求めたい距離は赤い線の部分です。
青く塗った直角三角形に注目すれば、力 F(θ) と、点 A との距離はDsinθ+Hcosθ です。
従って、F(θ) によるモーメントは
F(θ) ×(Dsinθ+Hcosθ)・・・(2)です。
静止しているのだから、(1)=(2)です。
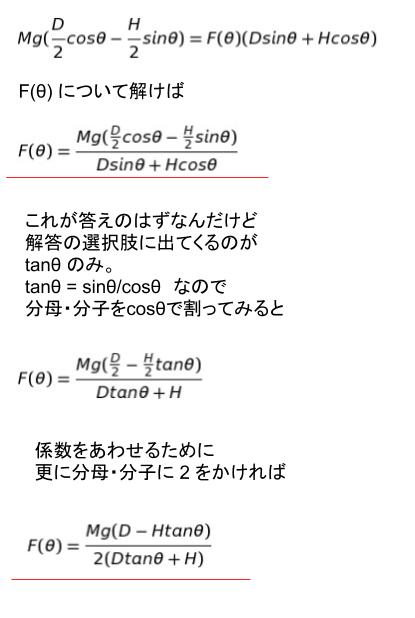
以上より、正解は 2 です。

コメント