問 題
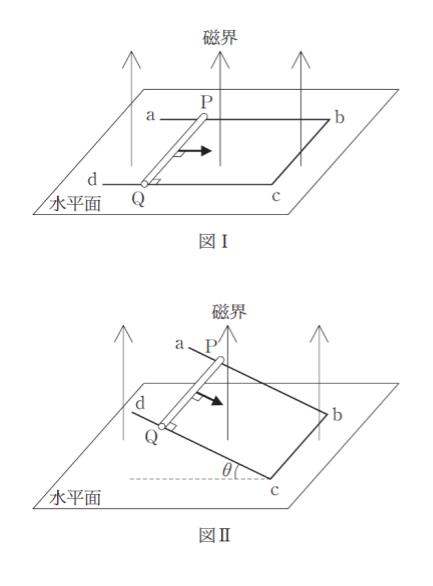
図Ⅰは水平面に対して平行に、図Ⅱは水平面に対して角度 θ (0< θ< π/2)傾いた状態で導線 abcd がそれぞれ配置されている。
各図共に大きさが等しい一定の速度で導体 PQ を導線 abcd に接した状態で動かすとき、図Ⅰで発生する誘導起電力 V1 と図 Ⅱ で発生する誘導起電力 V2 の比 V1/V2 として最も妥当なのはどれか。ただし、図Ⅰ及び図共に水平面と垂直で一様な等しい磁束密度の磁界が印加されており、また ab // dc である。
1.1/sinθ
2. sinθ
3.1/cosθ
4. cosθ
5.1
解 説
特殊な場合を考えます。 θ = 0 の時、当然 V1/V2 = 1 のはずです。であれば、θ → 0 の時、1 に近づくものが正解だろうと考えられます。従って、 3 ~ 5 です。
そして、θ → Π/2 の時ですが、θ = Π/2 の時を考えると、導体 PQ を動かしても、移動する方向と磁束の方向が一致しているため、単に同じ矢印によって貫かれていくだけです。つまり、貫く磁束の数が変化しません。変化がないので誘導起電力が生じないと考えられます。すると V2 → 0 となるので、V1/V2 → ∞ に近づくものが正解です。以上より、正解は 3 です。
ちなみに、この問題の設定は「磁場中にある閉回路の可動動線部分に力を与えて動かしたら、誘導起電力が生じて電流走る」という現象です。そして、電流が流れる回路部分の面積が変化することにより、貫く磁束変化→ファラデーの法則より、誘導起電力発生という流れです。
この時、一定速度を v、水平方向と 回路のなす角を θ と設定すると、誘導起電力 V = vBl cosθ が成立します。V = vBl cosθ を知識として覚えておくと、類題に対応しやすいのではないかと思われます。

コメント