問 題
幼なじみのA〜Fの 6人は、地元にある三つの高校のいずれか一つに通っている。この6人の文系又は理系の選択(文理選択)、部活動、カバンの色については、表のとおりである。

いま、この6人について次のことが分かっているとき、確実にいえるのはどれか。
○どの高校にも、理系選択者が少なくとも1人は通っている。
○サッカー部の者と書道部の者の両方が通っている高校はない。
○同じ色のカバンを持つ者が2人以上通っている高校はない。
- CとDは同じ高校に通っている。
- CとFは同じ高校に通っている。
- EとFは別々の高校に通っている。
- 1 人しか通っていない高校がある。
- 理系選択者が 2 人通っている高校には、文系選択者は通っていない。
正解 (5)
解 説
高校をそれぞれ、1高、2高、3高と名付けます。カバンの色が同じだと、違う高校ということなので、カバンの色が黒のA,D,Fをそれぞれ1高、2高、3高に通っているとしてみます。
すると、どの高校にも理系が1人はいるという条件から、3高に B or E が通っています。ところが、サッカーと書道は別なので、B は2,3高に通えません。よって、Bが1高、E が3高です。
残っているのは、Cですが、Cは 書道部と一緒にはなれないので、2高 or 3高に通うとわかります。表にまとめると、以下のようになります。
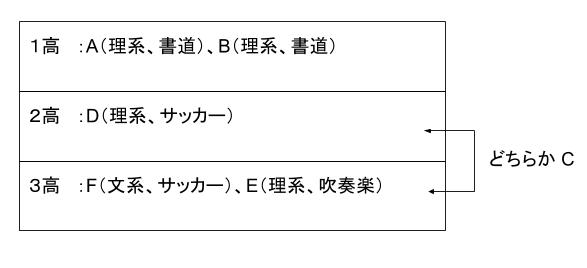
これをふまえて、各選択肢を検討すると
選択肢 1 ですが、C,Dは同じとは確定しません。
選択肢 2 ですが、C,Fは同じとは確定しません。
選択肢 3 ですが、E,Fは同じ高校に通っています。
選択肢 4 ですが、Cによります。
以上より、1~4が誤りなので、正解は 5 です。
ちなみに、選択肢 5 ですが、理系選択者が 2 人通っているのは、1高です。Cは 2 or 3高なので、確かに1高に文系選択者は通っていません。

コメント