問 題
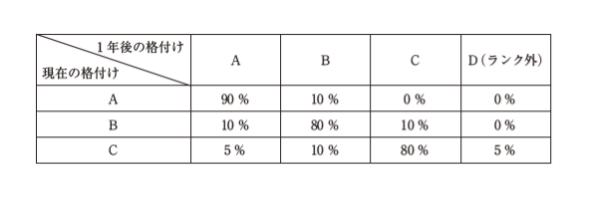
ある格付け会社は企業をA、B、C、D(ランク外)の段階で格付けしている。表は、この格付け会社によってA、B、Cに格付けされた企業が年後にどのような格付けになるかの確率を示したものである。
これによれば、現在Aに格付けされている企業が 4 年以内にD(ランク外)の格付けになる確率はいくらか。
ただし、いったんD(ランク外)の格付けになった企業が再びA、B、Cの格付けを得ることはないものとする。
1.0.1 %
2.0.125 %
3.0.15 %
4.0.175 %
5.0.2 %
正解 (4)
解 説
表を読むと、A→C、A→D、B→Dといった、2ランク以上、一気に下がる確率はないとわかります。従って「順々にランクが落ちて、3年後に D」か、「1回同じランクに留まって、4年後に D」の2パターンを考えればよいとわかります。
3年後に D、すなわち、A→B→C→D となる確率は 1/10 × 1/10 × 5/100 = 5/10000 です。
同じランクにとどまるのが、A→A、B→B、C→Cと考えられるので、それぞれのパターンの確率を考えます。
- A→A→B→C→Dとなる確率は 9/10 × 1/10 × 1/10 × 5/100 = 45/100000 です。
- A→B→B→C→Dとなる確率は 1/10 × 8/10 × 1/10 × 5/100 = 40/100000 です。
- A→B→C→C→Dとなる確率は 1/10 × 1/10 × 8/10 × 5/100 = 40/100000 です。
以上より、全部合わせると
(50+45+40+40)/100000
= 175/100000
= 0.175/100
なので、0.175% です。正解は 4 です。

コメント