問 題
構造物の振動に関する次の記述のア~ウに当てはまるものの組合せとして最も妥当なのはどれか。
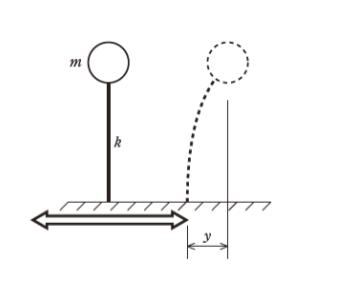
「質量 m の質点を自重を無視できるばね定数 k の柱で地盤に固定支持した減衰定数 h の構造物がある。図のように地盤が正弦波振動をして支点が変位したとき、支点から質点までの最大の水平距離が y であった。
このとき、ア で表される減衰がないときの構造物の固有振動数が地盤の振動の振動数よりも小さい場合は、k を イ すると、y を小さくすることができる。また、h を ウ してもy を小さくすることができる。
- ア、 イ、 ウ
- 1/2π √m/k、 大きく、 小さく
- 1/2π √m/k 、 小さく、 大きく
- 1/2π √k/m 、 大きく、 大きく
- 1/2π √k/m 、 小さく、 大きく
- 1/2π √k/m 、 小さく、 小さく
正解 (4)
解 説
ばね振り子の公式から、周期はT = 2π√m/k です。周期とは「1回振動するのに何秒かかるか」です。
一方、振動数(f)とは「1秒間に何回振動するか」 なのでf = 1/T で求めることができます。
従って、アは、(1/2π) × √k/m です。
地盤の振動の振動数よりも固有振動数が小さい場合は、その2つの振動数が近づくほど振動が強めあって振れ幅が大きくなると考えられます。
従って、振動数が小さい方が y が小さい → k が小さいと y が小さい と考えられます。イ は「小さく」です。
減衰定数については、より減衰する構造の方がy は小さくなるだろうと考えられます。よってh を「大きく」すると、y は小さくなります。
以上より、正解は 4 です。

コメント