公務員試験 H25年 国家一般職(電気・電子・情報) No.26解説

図Ⅰのような四端子回路において、電圧 V₁、V₂ 及び電流 I₁、I₂ を図の向きにとったとき、縦続行列は

で定義される。このとき、図Ⅱのような四端子回路において、縦続行列の要素 D に該当するものとして最も妥当なのはどれか。

1. 1
2. 2
3. 3
4. Z
5. 2Z

 

 

 

 

 

　解 説　　　　　

四端子行列では、電流と電圧をそれぞれ入力、出力に分けて表します。本問ではそれぞれ I₁,V₁、I₂,V₂ です。何を入力したら、何が出力されるかをうまく計算するための係数の集まりが、行列として表されている所です。行列のままだとまとまりすぎてよくわからないので、右辺を計算します。

A~Dを解くために、四端子行列でできることは、出力端子をつなげて（短絡して） V を 0 にする　か、出力端子を解放して I = 0 にする　です。※入力の V や I を 0 にしちゃうと、この回路に何も流れず意味がない。そのため出力側をいじります。
V₂ = 0 とすると 下の式から、I₁ = DI₂ です。

そして図Ⅱを見れば、Dは明らかに 3 です。これは以下のような回路を考えるとイメージしやすいのではないでしょうか。

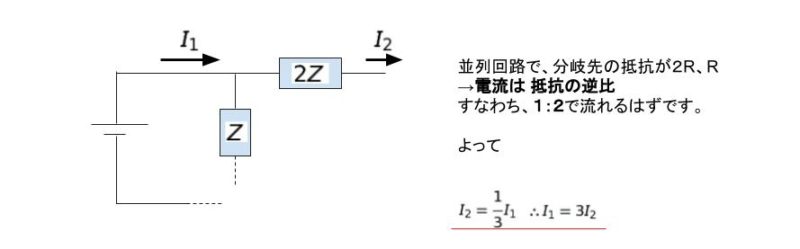
以上より、正解は 3 です。