公務員試験 H24年 国家一般職(教養) No.23解説

　問 題　　　　　

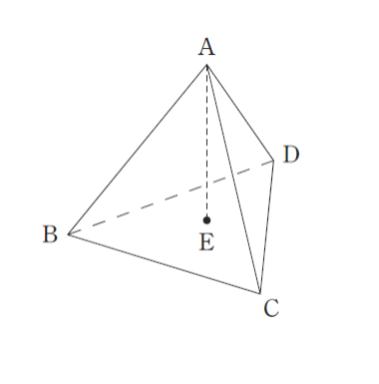
図のような正四面体 ABCD があり、点Ａから底面の三角形 BCD に向かって垂線を下ろし、その垂線と三角形との交点を E とする。線分 AE を含み辺 CD と平行な平面で正四面体 ABCD を切断するとき、点 Ｂを含む立体の体積と辺 CD を含む立体の体積の比はいくらか。

• 点B を含む立体の体積：辺CD を含む立体の体積

1. １ ： １
2. ２ ： ３
3. ３ ： ４
4. ４ ： ３
5. ４ ： ５

 

 

 

 

 

　解 説　　　　　

高さが等しい錐体が２つできるので、底面積の比がそのまま体積の比になります。三角形 BCD に注目し、点 E から CD と平行な補助線を引いて考えます。平行な補助線と BC,BD との交点をそれぞれ F,G とおきます。点 E は正三角形の重心になるため、 BF：FC や BG：GD 等はすべて ２：１ です。

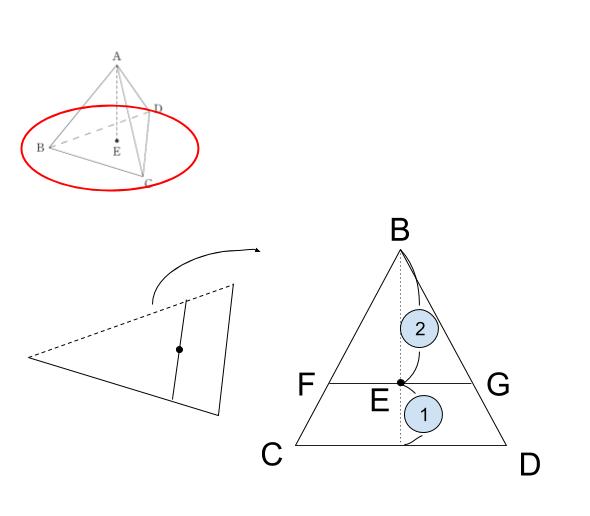
⊿ BFG と ⊿ BCD は相似です。相似比は 2：３です。従って、面積比は ４：９です。

２つの立体の底面積の比は、⊿ BFG ：□CDGF  = ４：５となります。従って、正解は 5 です。