問 題
長方形断面の水路を流れる一様な開水路の流れにおいて流量 Q で一定とした場合、比エネルギー E と水深 h の関係は図中の点 A,B を通る実線のようになった。
この関係に関する記述ア~ウの正誤の組合せとして最も妥当なのはどれか。
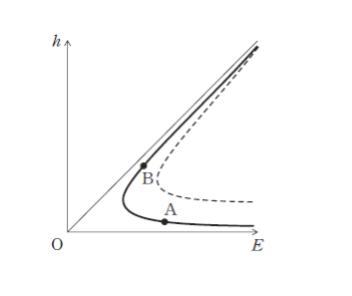
ア 点 A で表される流れは常流である
イ 同じ水路において流量を Q1 としたときの比エネルギー E と水深 h の関係は図中の点線のようになった。このとき、Q < Q1 である。
ウ 点 B で表される流れから点 A で表される流れに遷移するとき、跳水現象が発生する
- ア イ ウ
- 正 正 誤
- 正 誤 正
- 誤 正 正
- 誤 正 誤
- 誤 誤 正
正解 (4)
解 説
比エネルギーとは、開水路において水路床を基準にとったときの全エネルギーを水頭の形で表したものです。
ポイントは、流量を一定とした時に水深Qと比エネルギーEについて、特徴的なグラフがかけることです。(本問の図)
このグラフから読み取るべきポイントは「比エネルギーが最小になる時の、水深」です。これを「限界水深」といいます。これよりも水深が低いと、射流、高いと常流です。
限界水深は3√(Q2/gB2) で求めることができます。ちなみに、B は、断面の幅です。
以上をふまえて、各選択肢を検討します。
記述アは誤りです。射流です。
記述 イ は、正しい記述です。限界水深が上がっています。この時、流量 Q は増えているはずです。
記述ウは誤りです。B→Aなので、常流→射流です。この際跳水現象は発生しません。跳水現象は、射流→常流の際に発生します。
従って、誤、正、誤です。
正解は 4 です。

コメント