問 題
ある工場では、 2 種類の製品A、Bを製造しており、その製造に要する時間は、それぞれ1 個当たり、常に次のとおりである。
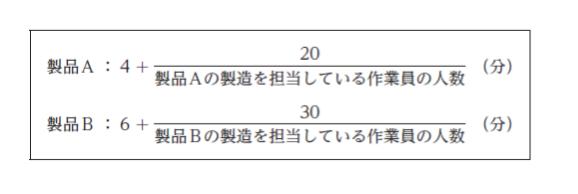
ある日、この工場では、合計60 人の作業員を製品A、Bのいずれか一方の製造の担当に振り分けて同時に製造を開始したところ、 4 時間後の時点で、この日に製品Bを製造した個数がちょうど35 個となり、製造を一時停止した。
製品Aの製造を担当する作業員を新たに何人か追加して製造を再開したところ、再開して2 時間20 分後に、この日に製品Aを製造した個数がちょうど80個となり製造を終了した。
この日、製品Aの製造を担当する作業員を新たに追加した後、製品Aの製造を行っていた作業員の人数は何人か。ただし、作業員は、担当となった種類の製品の製造のみを行うものとする。
1. 28 人
2. 30 人
3. 32 人
4. 34 人
5. 36 人
解 説
問題文前半の「4時間で製品 B 35個できた」という点から考えます。
4時間 = 240 分なので、1個あたり 240/35 = 48/7 = 6 + 6/7 分 で製造しています。 問題文の表の、製品 B の行に注目すると、分子が 30 です。そこで、分子をそろえてみると 「6 + 30/35」 です。従って、 35 人で B を担当していたとわかります。
従業員は 60 人なので、A には 25 人が担当していました。すると、1 個あたり 4 + 20/25 分 = 4 + 4/5 分で製造していたとわかります。240分で製造したのは 「240 ÷ (4 + 4/5)」 = 「240 × 5/24」 = 50 個です。
その後、再開して 2 時間 20 分 = 140 分で ちょうど 80 個になっているので、この 140 分で 製品 A は 30 個製造されています。 1個あたり 140 ÷ 30 = 14/3 = 4 + 2/3 = 4 + 20/30 分です。問題文の表の、製品 A の行に注目すれば、作業員の人数は 30 人とわかります。
以上より、正解は 2 です。

コメント