問 題
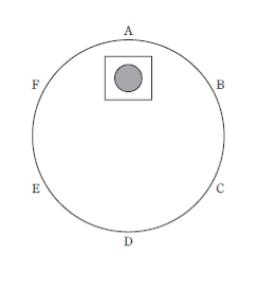
図のようにA~Fの6人が丸いテーブルを囲みテーブルの中心を向いて座っており,次のようなルールで皿を移動させながら、皿に置かれたパンケーキの上に「が」「ん」「ば」「れ」「日」「本」と1文字ずつチョコレート・クリームで書くこととした。
① 皿を渡されたら「が」「ん」「ば」「れ」「日」「本」の順に1文字書く。
② 1文字書いたらコインを1枚投げ表が出たら右隣の人に裏が出たら左隣の人に皿を渡す。
③ 6文字書き終わるまで皿を渡し続ける。
このルールに基づいてまずAが「が」の文字を書いてから皿を移動させるときBが最後の文字「本」を書く確率はいくらか。
1. 1/8
2. 1/5
3. 1/4
4. 5/16
5. 11/32
正解 (5)
解 説
Aから「右」とは、A→F→E・・・の方向です。これを「+」とします。
Aから「左」とは、A→B→C・・・の方向です。これを「ー」とします。
5回のコインを投げた結果を、表1回→「+1」、裏1回→「-1」とすれば、5回分の結果を足して「-1」になれば、最後の文字である「本」を B が書くことになります。
また、全て表だった場合も、最後の文字である「本」を B が書くことになります。
従って、「表が2回、裏が3回出る確率+すべて表が出る確率」が求める答えです。
すべて表が出る確率は (1/2)5です。
また、表表裏裏裏と出る確率は (1/2)5です。そして裏が3個入る場所が 5C3 = 10 通りあります。
以上より、求める確率は (1/2)5 +(1/2)5 ×10 = 11/32 です。
正解は 5 です。

コメント