問 題
図のような直線上において、ある物体が点 O を中心として、周期 12s、振幅 1.0 m で単振動をしている。
この物体が点 C から点 A まで移動するのにかかる時間は次のうちではどれか。
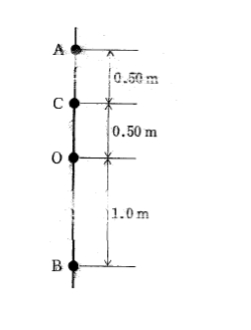
1 0.50s
2 1.5s
3 2.0s
4 3.0s
5 6.0s
正解 (3)
解 説
考え方1:
周期が 12s なので「O→A→O→B→O」の一往復で 12s かかる。よって「O→A→O」は6s のはずである。さらに「O→A」は 3s のはずである。
以上より、C → A は 3s よりは小さいと考えられます。選択肢 4,5 は誤りである。
次に、単振動のO→A間での物体の移動及び速度の変化をイメージすると、等速ではなく「O に近いほど速くA に近いほど止まりかけで遅い」と考えられます。
よって、O→C は3s の半分である 1.5s より短い時間しかかからず、『C→A は3s の半分である 1.5s より長い時間かかる』はずです。
選択肢の中で 1.5s ~ 3.0s となるのは、選択肢 3 のみである。
考え方2
単振動を、等速円運動に対応させて考える。角度を ω として
- 点Oに対応するω = 0
- 点Cに対応するω = 30° (もしくは π/6 ラジアン)
- 点Aに対応するω = 90° (もしくはπ/2 ラジアン)です。
等速円運動なので C→Aにかかる時間は、O→Cの2倍です。また、周期が 12s だから O → A は3s です。
以上より、C→Aは 2s とわかります。
正解は 3 です。

コメント