問 題
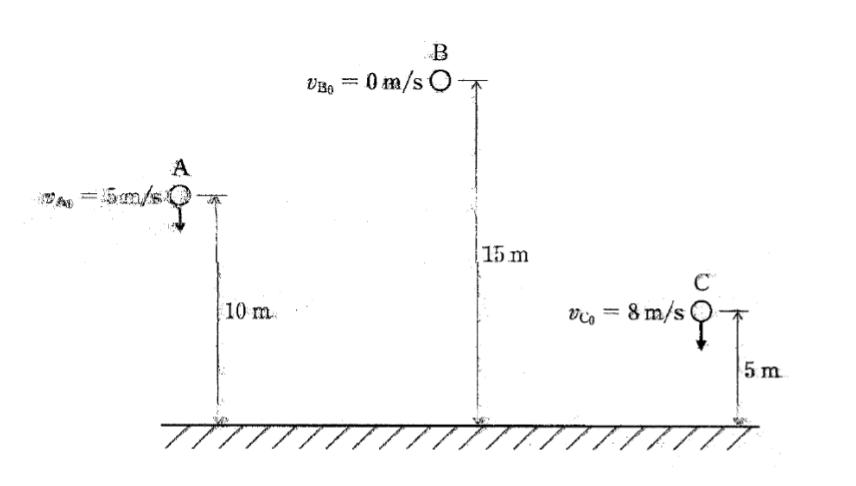
図のように三つの小球 A、B、C を、それぞれ10m、15m、5m の高さから鉛直下向きに初速度 vA0 = 5m/s、vB0 = 0m/s、vC0 = 8m/s で落下させたとき、地面に到達する直前の小球の速度の関係として最も妥当なのはどれか。
ただし、小球 A,B,C が地面に到達する直前の速度をそれぞれ vA、vB、vC とし、重力加速度の大きさを 10m/s2 とする。
1 vA < vB < vC
2 vB < vA < vC
3 vB < vC < vA
4 vC < vA < vB
5 vC < vB < vA
正解 (4)
解 説
高さが与えられているので、位置エネルギー及び力学的エネルギーについて考えます。
知識として
- U(位置エネルギー)= mgh
- K(運動エネルギー)= 1/2 mv2
- E力(力学的エネルギー)= U+K です。
また、A,B,C の質量が与えられていないため全て 1kg と仮定して、まず、落下させる時の A,B,C が持つ力学的エネルギーを以下、求めていきます。
A の力学的エネルギーは
1×10×10 + 1/2 × 1 × 52 = 112.5
B の力学的エネルギーは
1×10×15 = 150
C の力学的エネルギーは
1×10×5 + 1/2 × 1 × 82 =82 です。
さて、地面に到達する時、力学的エネルギーは保存され、かつ位置エネルギーは0です。
従って、それぞれの小球に関して
1/2 vA2 = 112.5
1/2 vB2 = 150
1/2 vC2 = 82 が成り立ちます。
よって
vA2 = 225
vB2 = 300
vC2 = 164 だから
vC < vA < vB となります。
以上より、正解は 4 です。

コメント