公務員試験 2019年 国家一般職(高卒 技術) No.18解説

　問 題　　　　　

16 進法で 16 と表される数を 2 進法で表したときの桁数はいくらか。

1． 4
2． 5
3． 6
4． 7
5． 8

 

 

 

 

 

　解 説　　　　　

n 進数の１桁目は n⁰ が何個あるかを示します。以下、2 桁目は n¹ が何個あるか、３桁目は n² が何個あるか・・・です。

16 進数で 16 なので、16⁰ が ６個、16¹が１個 → 1 × 6 + 16 × 1 = 22　です。

選択肢 1 が正解とすると
22 を２進数に直した時に、桁数が 4 です。2 進数の ４桁の場合、最大は 1111 です。これは 2³ + 2² + 2¹ + 2⁰ = 15 なので、22 には足りません。選択肢 1 は誤りです。

選択肢 2 が正解とすると
22 を 2 進数に直した時に、桁数が 5 です。２進数の 5 桁の場合、最大は 11111 です。これは 2⁴ + 2³ + 2² + 2¹ + 2⁰ = 31 です。従って、5 桁とわかります。

ちなみに
22 を　2 進数に直すと、10110 です。一般的に 10 進数表記されている数を、n 進数に直すためには、n で割って余りを書いていき、逆 L 字に読むと直せます。22 であれば、以下のようになります。

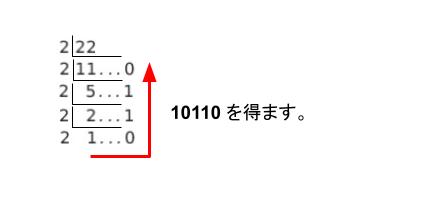
以上より、正解は 2 です。
類題 H27no18