2022年 国家一般職(高卒 技術) No.61 土木基礎力学　解説

　問 題　　　　　

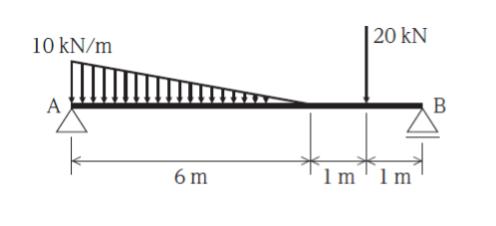
図のように、単純梁に鉛直集中荷重と等変分布荷重が作用しているとき、支点 A の鉛直反力の大きさとして最も妥当なのはどれか。ただし、梁の自重は無視するものとする。

1．20 kN
2．25 kN
3．30 kN
4．35 kN
5．40 kN

 

 

 

 

 

　解 説　　　　　

まず、荷重を１つにまとめます。

【三角形分布荷重 → 集中荷重】
等辺分布部分は、最終的に力が０の三角形分布であることが、見てわかります。三角形分布は、重心への集中荷重に変換します。力の大きさは面積なので、(10kN/m × 6m)/2 = 30 kN です。 

【２つの集中荷重 → 1 つの集中荷重】

２つの集中荷重をまとめて合力として表したものが、赤色の矢印です。50 kN の集中荷重が 単純梁のちょうど真ん中にかかるとわかります。2 つの集中荷重の大きさの比が 30 kN：20 kN = 3：2 なので、１つにまとめた集中荷重は 「2：3 に CD を分ける点」に作用します。

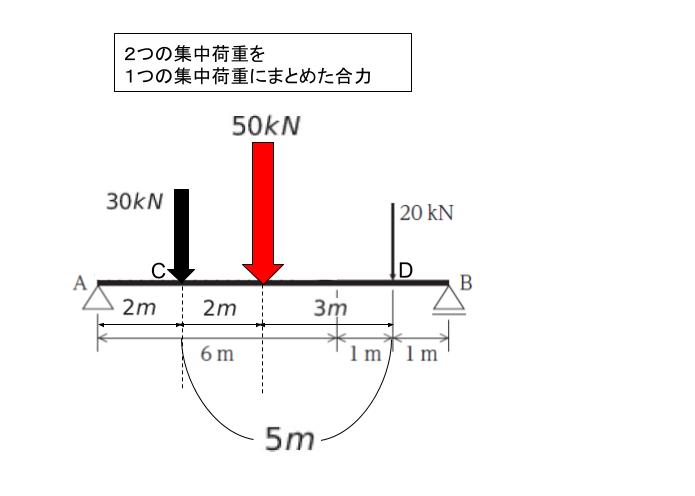
対称性より、R_A = R_B で、縦の力の和が０だから R_A + R_B = 50 です。従って、R_A = R_B = 25　kN です。

以上より、正解は 2 です。

類題 2019 no61 単純梁の反力