問 題
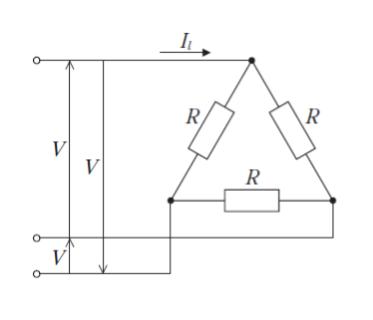
図のような三相交流回路において
線間電圧が V,各相の負荷が抵抗値 R の抵抗であるとき,線電流 Il の大きさとして最も妥当なのはどれか。
解 説
三相交流回路とは
単純な交流回路が3つ組み合わさっているものです。実体としては、回転する棒磁石が中心にあって、120°ずつずらしたコイルを置いていると考えればよいです。
線間とは、3つのうち2つの間ということです。
相というのが、3つある回路のうち、それぞれの回路と考えればよいです。
三相交流回路は
電源側と負荷側という 2 つのフィールドがあります。電源側の回路図には、交流電圧が3つ書かれて、大体 △ か Y につながっています。負荷側には、3つの抵抗が置かれて、大体 Δ か Y につながれます。この Δ と Y はそれぞれ変換することができます。その際、電圧や電流について変換が必要になります。
三個の回路を同時に考えるのは難しいため、三相交流回路において、線間電圧とか相電圧が出てくる計算問題の定石は Y – Y を考えるです。すると、1相分を抜き出した簡単な等価回路を考えることができます。ここまで、三相交流回路について、および考え方の一般的概要です。
本問では、負荷側が Δ でつながっています。そこで Y に変換します。負荷側の Δ ー Y 変換では、抵抗が 1/3 になります。つまり、もともと各抵抗が R だったので、R/3 となります。これは知識です。
次に、電源側は問題文に指定がないため、Y につながっているとします。電源側を Y につないでいる時、線間電圧は、相電圧の √3 倍です。これも知識です。従って、線間電圧が V であれば、相電圧は V/√3 となります。
問われているのが、線電流なので、単相における電流を考えればよいです。Y – Y でつないでしまえば、1相分を抜き出した 簡単な等価回路が得られます。抵抗が R/3 で、電圧が V/√3 です。I = V/R = √3× V/R を得ます。
以上より、正解は 4 です。

コメント