問 題
ガス燃焼の予混合気では、未燃混合気側に火炎面はある速度v(m/s)で移動し、その速度を予混合気の燃焼速度vという。火炎面は、混合気の流速とこの燃焼速度がつり合う位置に見かけ上静止する。
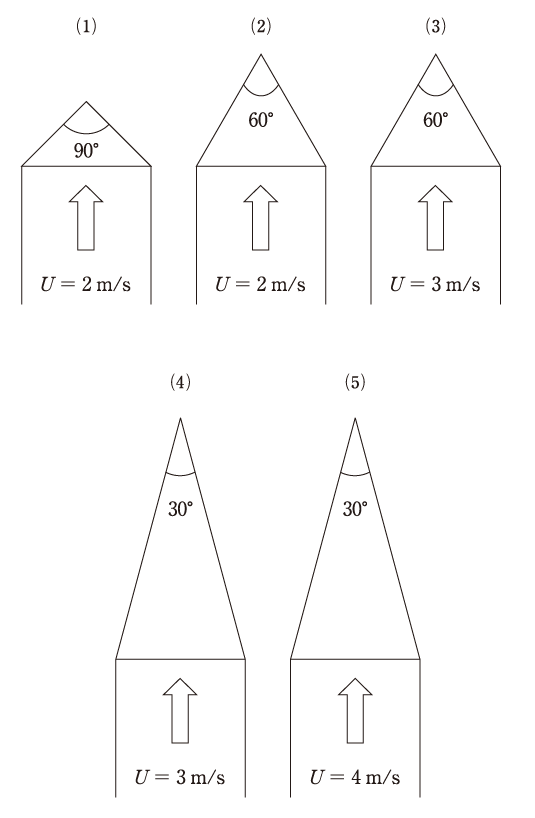
条件の異なる予混合気をスリット状の噴出口から、流速U(m/s)で流出させたとき、下図に示すように噴出口の上部に火炎面が二等辺三角形の等しい2辺となる平面状の火炎が形成された。
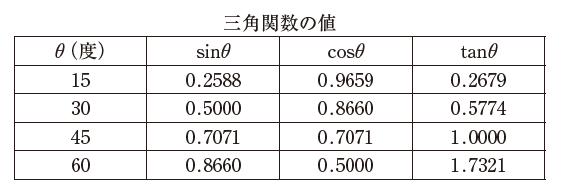
予混合気の流速Uと頂角が図に示される値であるとき、燃焼速度v(m/s)が最も大きいものはどれか。必要なら、表の数値を用いて良い。
解 説
本問は、設問の質という観点では難しい問題ではありませんが、少なくとも過去15年以上類題が見られないという、かなりマニアックなテーマを扱っています。そのため、もし本番でこのような設問に出会ったら、数分考えてみて解法が思いつかなければ、捨て問題と見なしてしまって構わないと思います。
まず、問題文より、火炎面が二等辺三角形の形で見かけ上静止しています。これは、たとえば火炎面のある点に注目したとき、燃焼速度v[m/s]のベクトルと、混合気の流速U[m/s]のうち火炎面に垂直な成分のベクトルがつり合っていることを意味します。
言葉だとわかりにくいので、下図(A点でのつり合いを表すベクトル図)を参照してください。なお、ここでは二等辺三角形の頂角をθ[°]としています。
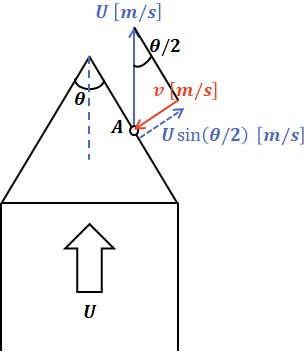
このA点において、vとUsin(θ/2)のバランスが崩れてしまうと火炎面が動くことになります。実際には火炎面は静止していることから、以下に示す式が成り立ちます。
![]()
問われているのは、選択肢(1)~(5)で与えられる様々なUやθに対するvの大きさの比較です。そこで、選択肢(1)~(5)に対応するvの値(v1~v5)を計算すると、それぞれ次のようになります。
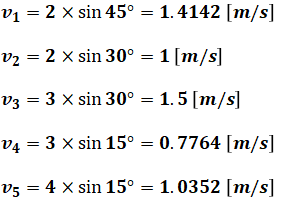
以上から、最大となるのはv3=1.5[m/s]なので、正解は(3)です。

コメント