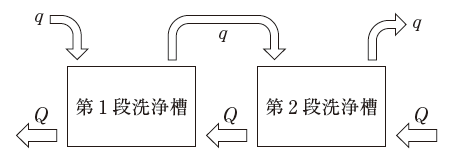
図に示す向流二段洗浄において、各段の洗浄水量Qを1m3/min、製品が各段で持ち込む水量q、持ち出す水量qをそれぞれ10L/minとするとき、単位時間当たりに第1段洗浄槽に入る製品に付着する不純物質の量a0に対する第2段洗浄槽を出る製品に付着する不純物質の量a2の比(a2/a0)の値に最も近いものはどれか。
- 1/100
- 1/1000
- 1/10000
- 1/100000
- 1/1000000
正解 (3)
解 説
1m3は1000Lなので、第1段洗浄槽では10Lの汚水を1000Lの洗浄水で洗うため、不純物質の濃度は約100分の1に薄まります(正確には10/1000ではなく10/1010で計算するべきですが、選択肢を見るとそこまで厳密に考える必要はありません)。
第2段洗浄槽でも同様に汚水10Lに対して洗浄水を1000L使っているため、ここでも不純物質の濃度は約100分の1に薄まります。
以上から、最初の不純物質の量a0に対し、第2段洗浄槽を出るときの不純物質の量a2は、100分の1のさらに100分の1となるので、(3)の1/10000が正解です。
ちなみに、この問題はそれぞれの選択肢の値が大きく異なっているため、このような概算によって正解を選ぶことができました。もし選択肢同士の値が近い場合には、大雑把な計算ではなく正確な数値を算出しなくてはなりません。
その場合の解法については、R2年 問2の解説を参考にしてください。

コメント