接触凝集沈殿装置の性能を表す凝集速度式として、正しいものはどれか。
ここに、nは原水に凝集剤を注入してできた微小フロックの単位体積中の個数(個/cm3)、Nは既成フロックの単位体積中の個数(個/cm3)、Dは既成フロックの直径(cm)、ε0は水の単位体積中で単位時間に消費される攪拌エネルギー(erg/(cm3・s))、μは水の粘性係数(g/(cm・s))である。
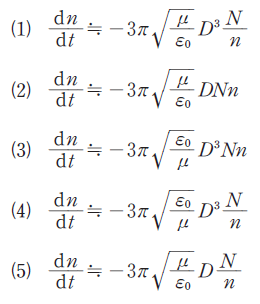
正解 (3)
解 説
凝集速度式を公式として身につけていればこの問題は答えができます。けれど、この式は近似値でそこまで確固たる公式でない上、特に頻出でもないため、正確に覚えている方は少ないかもしれません。そのような場合は、選択肢の中から、もっともそれらしいものを選ぶことになります。
まず、左辺はすべて同じですが、フロックの個数と時間の比なので、これは凝集速度を表します。
次に、右辺の√の中を見ると、μが分子にある選択肢と分母にある選択肢があります。μは粘性係数ですが、粘性が大きいと水が混ざりづらくなる=凝集剤も混ざりづらくなるので、凝集速度は下がります。よって、μは分母にきます。μが分母だとε0は分子になりますが、これは攪拌エネルギーが大きいほど水も凝集剤もよく混ざって凝集速度が上がるためです。
D、Nは既成フロックの直径と数、nは微小フロックの数ですが、既成フロックと微小フロックがくっついて大きなフロックとなるため、なるべく直径が大きくて数が多いほうが、両者の接触機会が多くなるので、凝集速度も大きくなります。よって、D、N、nはすべて分子にきます。
以上のように考えると、3πや√や3乗の意味を理解したり公式として暗記したりしなくても、答えを出すことができます。

コメント