R2年 汚水処理特論 問2 問題と解説

　問 題　　　　　

3段の向流多段洗浄において、製品が各段で持ち出す水量(v)を半減させて、洗浄水量(V)との比(V/v)を5から10に上げることにより、第3段の洗浄槽を出る製品中の不純物質の量を、およそ何分の1に減少させることができるか。

1. 1/2
2. 1/4
3. 1/5
4. 1/7
5. 1/10

 

 

 

 

 

　解 説　　　　

この問題はH30年 問1に似た出題ですが、選択肢の値がそれぞれ近いため、H30年 問1の解説に示したような概算で正解を得る方法が使えません。そのため、向流多段洗浄の洗浄性能を表す公式を使ってしっかり計算していくことになります。

ただし、これは出題頻度から見ても重要な公式というわけではないので、もし難しいようなら捨て問題扱いとしてしまっても構わないと思います。とりあえず以下の解説を読んでみて、余裕があれば知識として押さえておいてください。

---

n段の向流多段洗浄の様子を図示すると、次のようになります。

• a₀：原料に含まれる不純物の量
• a_n：製品に含まれる不純物の量
• v：製品が各段で持ち出す水量
• V：洗浄水量
• r：V/v (洗浄水量Vと製品が各段で持ち出す水量vの比)

上図において、「原料に含まれる不純物の量」に対する「製品に含まれる不純物の量」の比は、以下の式で表すことができます。

今回は3段なので、初めの条件(V/v=5)を上式に当てはめると次のようになります。

また、後の条件(V/v=10)を上式に当てはめると次のようになります。

よって、これらの比を求めることで、不純物質の量がどれくらい少なくなったか計算することができます。

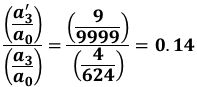
ここで選択肢を見ると、(3)の1/5が0.20、(4)の1/7が0.14、(5)の1/10が0.10なので、正解は(4)と判断できます。