電験三種 R4年度上期 機械 問8 問題と解説

　問 題　　　　　

単相変圧器の一次側に電流計、電圧計及び電力計を接続して、短絡試験を行う。

二次側を短絡し、一次側に定格周波数の電圧を供給し、電流計が40Aを示すように一次側の電圧を調整したところ、電圧計は80V、電力計は1000Wを示した。

この変圧器の一次側からみた漏れリアクタンスの値[Ω]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし、変圧器の励磁回路のインピーダンスは無視し、電流計、電圧計及び電力計は理想的な計器であるものとする。

1. 0.63
2. 1.38
3. 1.90
4. 2.00
5. 2.10

 

 

 

 

 

　解 説　　　　

変圧器で無負荷試験と短絡試験を行うのは、無負荷損(≒鉄損)と負荷損(≒銅損)を知るためです。無負荷試験により無負荷損(≒鉄損)がわかり、短絡試験により負荷損(≒銅損)がわかります。今回は、このうち短絡試験からの出題となります。

問われているのは「変圧器の一次側からみた漏れリアクタンスの値」なので、まずは、単相変圧器の二次側の諸量を一次側に換算した簡易等価回路を描くことから始めます。

この手の問題はたびたび出題されているので、問題文に図がなくても以下のような等価回路を描けるようにしておく必要があります。この作業に慣れていない方は、変圧器の等価回路のページやH26年 問7の解説を確認しておいてください。

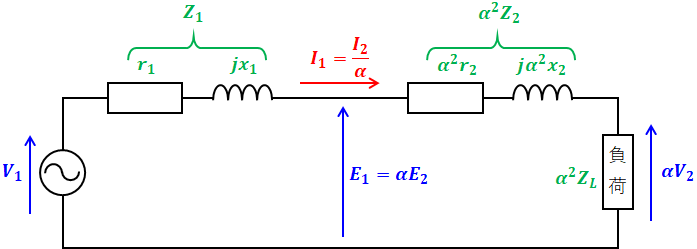
• V₁、V₂：一次電圧、二次電圧 [V]
• E₁、E₂：一次側、二次側の誘導起電力 [V]
• I₁、I₂：一次電流、二次電流 [A]
• r₁、r₂：一次巻線、二次巻線の抵抗 [Ω]
• x₁、x₂：一次巻線、二次巻線の漏れリアクタンス [Ω]
• Z₁、Z₂：一次巻線、二次巻線のインピーダンス [Ω]
• Z_L：負荷インピーダンス [Ω]
• α：巻数比 (N₁/N₂)

なお、今回は二次側を短絡しているので、負荷Z_Lはありません。また、短絡試験では巻線比など関係なしに、一次側と二次側を合わせた電流・電圧・電力が計測されるため、上図の等価回路をさらに簡略化して、下図のように描くことができます。

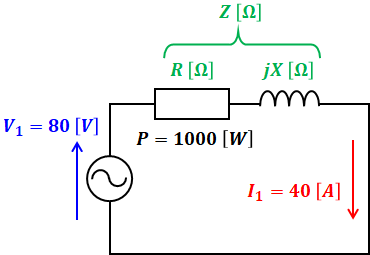
• V₁：一次電圧 [V]
• I₁：一次電流 [A]
• R：一次側からみた合成巻線抵抗 [Ω]
• X：一次側からみた合成漏れリアクタンス [Ω]
• Z：一次側からみた合成インピーダンス [Ω]
• P：銅損 [W]

上図において、Xを求めるのが最終目標です。

最初に、V₁、I₁の値が既知なので、ここからZの大きさを計算することができます。

さらにPの値もわかっているので、ここからRが算出できます。

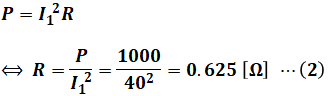
(1)式と(2)式でZとRがわかったので、三平方の定理を使えば求めたいXを算出することができます。

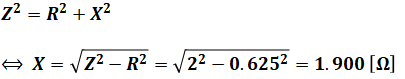
よって、正解は(3)となります。