問 題
次の文章は、水車の比速度に関する記述である。
比速度とは、任意の水車の形(幾何学的形状)と運転状態(水車内の流れの状態)とを( ア )変えたとき、( イ )で単位出力(1kW)を発生させる仮想水車の回転速度のことである。
水車では、ランナの形や特性を表すものとしてこの比速度が用いられ、水車の( ウ )ごとに適切な比速度の範囲が存在する。
水車の回転速度をn[min-1]、有効落差をH[m]、ランナ1個当たり又はノズル1個当たりの出力をP[kW]とすれば、この水車の比速度nsは、次の式で表される。
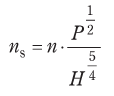
通常、ペルトン水車の比速度は、フランシス水車の比速度より( エ )。
比速度の大きな水車を大きな落差で使用し、吸出し管を用いると、放水速度が大きくなって、( オ )やすくなる。そのため、各水車には、その比速度に適した有効落差が決められている。
上記の記述中の空白箇所(ア)、(イ)、(ウ)、(エ)及び(オ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
(ア) (イ) (ウ) (エ) (オ)
- 一定に保って有効落差を 単位流量(1m3/s) 出力 大きい 高い効率を得
- 一定に保って有効落差を 単位落差(1m) 種類 大きい キャビテーションが生じ
- 相似に保って大きさを 単位流量(1m3/s) 出力 大きい 高い効率を得
- 相似に保って大きさを 単位落差(1m) 種類 小さい キャビテーションが生じ
- 相似に保って大きさを 単位流量(1m3/s) 出力 小さい 高い効率を得
解 説
水車の比速度とは、実物の水車を相似形で縮小した仮想水車に対し、1[m]の落差で1[kW]の出力を生じさせるときの回転速度[min-1]のことです。要するに、水車には様々な大きさや形状のものがありますが、その能力を比較するために単位高さ・単位出力あたりの回転速度を求めることで、基準を揃えた能力を知ることができる、というわけです。
よって、( ア )には「相似に保って大きさを」が、( イ )には「単位落差(1m)」が入ります。
また、この問題では問題文で比速度の式が示されていますが、もし式を与えられていなくても、重要公式として使えるようにしておくべきです。
比速度は大きすぎず小さすぎず、適正な範囲で運用することが重要です。この「適正な範囲」というのは水車の種類によって異なります。適正な比速度が大きい順に並べると、以下のような大小関係が成り立ちます。
(比速度:大) プロペラ水車 > 斜流水車 > フランシス水車 >ペルトン水車 (比速度:小)
よって、( ウ )には「種類」が、( エ )には「小さい」が入ります。
( オ )を含む文章を見ると、比速度の大きな水車を大きな落差で使用し、放水速度が大きくなっているという状況です。
このような場合、水中の気泡が大きな圧力で押しつぶされ、ランナなどの設備に衝撃を与えて損壊させるおそれがあります。この現象をキャビテーションといい、これは水車を痛める原因となるので、比速度や有効落差を適正な値に設定することで、キャビテーションを起こさないようにすることが重要です。
よって、( オ )には「キャビテーションが生じ」が入ります。
以上から、
- 相似に保って大きさを
- 単位落差(1m)
- 種類
- 小さい
- キャビテーションが生じ
となるので、正解は(4)です。

コメント