問 題
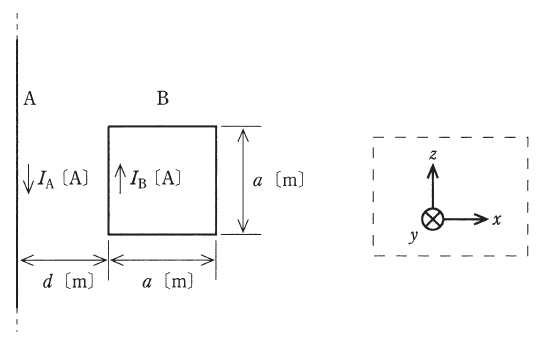
図のように、透磁率μ0[H/m]の真空中に無限に長い直線状導体Aと1辺a[m]の正方形のループ状導体Bが距離d[m]を隔てて置かれている。AとBはxy平面上にあり、Aはz軸と平行、Bの各辺はx軸又はz軸と平行である。A、Bには直流電流IA[A]、IB[A]が、それぞれ図示する方向に流れている。
このとき、Bに加わる電磁力として、正しいものを次の(1)~(5)のうちから一つ選べ。
なお、xyz座標の定義は、破線の枠内の図で示したとおりとする。

解 説
Bに加わる電磁力が問われていますが、Bは正方形をしているので、直線の導体が4本あるとして分けて考えます。
わかりやすいのがBの正方形のうち、上辺と下辺です。上辺は電流が紙左から右へと流れ、下辺は右から左へと流れていているので、向きが反対です。そしてAからの距離は上辺も下辺も同じなので、上辺に加わる電磁力と下辺に加わる電磁力は、大きさが全く同じで、符号が反対ということになります。よって、この2辺分だけを考えると、その合力は0です。
次に正方形の左辺と右辺を考えます。これらも流れる電流の向きが違うので、加わる電磁力の符号が反対になりますが、Aの導体からの距離も異なるため、加わる電磁力の大きさも変わってきます。電磁力の式は以下の通りです。
![]()
- F:反発力 [N]
- μ:透磁率 [H/m]
- I:電流 [A]
- l:導線の長さ [m]
- d:導体間距離 [m]
左辺については、この式のdはdのまま、lはaになります。右辺については、この式のdがd+aになり、lはaになります。符号は上記の通り反対になるので、合力はこれらの差を求めればよいです。

よって、答えが(2)と(3)に絞られます。
最後に力の向きを決めます。
導体Aの電流の向きは紙面上から下で、これにより発生する磁界の向きは右ねじの法則に従います。そのため、導体Aよりも右側にある導体Bのところでは、磁界の向きは奥側から手前側へと向かう方向となります。
すると、導体Bを流れる電流の向きは問題の図で与えられているので、あとはフレミングの左手の法則を使えば、力の向きがわかります。
つまり、導体Bの左辺に注目すると、電流は下から上、磁界は奥から手前なので、働く力の向きは右向き、つまり+x(正)の方向となります。一方、導体Bの右辺に注目すると、電流は上から下、磁界は奥から手前なので、働く力の向きは左向き、つまり-x(負)の方向となります。
ただし、すでに示した電磁力の式からもわかる通り、導体間距離が近いほど電磁力は大きくなるので、右辺よりも左辺の影響のほうが大きいことがわかります。よって、全体で考えると、導体Bに加わる電磁力は+x(正)の方向であると判断することができます。
以上から、正解は(2)となります。

コメント