問 題
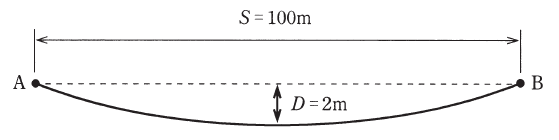
図のように高低差のない支持点A、Bで支持されている径間Sが100[m]の架空電線路において、導体の温度が30[℃]のとき、たるみDは2[m]であった。
導体の温度が60[℃]になったとき、たるみD[m]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、電線の線膨張係数は1[℃]につき1.5×10-5とし、張力による電線の伸びは無視するものとする。
- 2.05
- 2.14
- 2.39
- 2.66
- 2.89
正解 (3)
解 説
電線のたるみに関する計算問題はたびたび出題されているので、以下の2つの式は公式としてぜひ覚えておきたいところです。一つは電線のたるみD[m]を求める式、もう一つは電線の長さL[m]を求める式です。
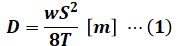
- D:電線のたるみ [m]
- w:荷重(電線1mあたり) [N/m]
- S:電線の支持物間の距離(径間長) [m]
- T:水平張力(電線の水平方向) [N]
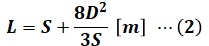
- L:電線の長さ [m]
今回はすでにD=2[m](30℃)と与えられているので、1つ目の式は使わず、2つ目の式だけで解くことができます。2つ目の式に問題文で与えられた数値を代入すると、以下のように計算できます。
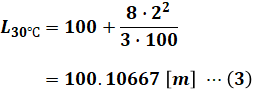
- L30℃:30℃条件下での電線の長さ [m]
導体の温度が60℃になると、1℃につき、もとの長さの1.5×10-5倍した分だけ膨張するので、
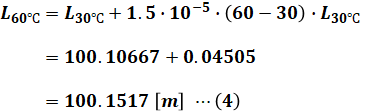
- L60℃:60℃条件下での電線の長さ [m]
となります。よって、60℃条件下でのたるみD[m]は、再度2つ目の公式に数値を代入していくと得ることができます。
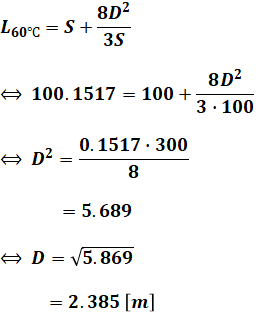
以上から、正解は(3)となります。

コメント
(4)式の下の文
L60℃:・・・のところ、「60℃条件下での電線の長さ」が正しい文ではないでしょうか?
修正しました。ご指摘ありがとうございます!