【1-コンパートメントモデル】
コンパートメントとは、仕切った区画のことです。1-コンパートメント(以下、「1-コンパ」と略します。 )とは、人体を1つの四角い部屋に例えて、薬物投与量と消失を考えるモデルです。
1-コンパで重要な仮定は「投与薬物が体循環血に入ると、0秒で全体に分布する」です。投与薬物が体循環血に入るのは「静脈から薬を注射」する場合が一番簡単なパターンです。
錠剤や散剤を飲んだ場合(「経口投与、1-コンパ」)では、吸収するまで体循環に入らない点に注意します。また、経口の場合、投与量全てが体循環に入るわけではありません。この割合が、バイオアベイラビリティです。詳しくみるなら『消化管吸収を受ける → 消化管壁における代謝を受ける → 門脈経由でまず肝臓へ。肝で代謝(肝初回通過効果)をうける。 → ようやく体循環へ』 という過程を経ます。経口の1-コンパとは、以上のような過程を経た後、体循環に入れば、一瞬で分布するというモデルです。
【1-コンパ 薬物の消失速度】
薬物の消失速度(-dX/dt)は、「線形」が基本です。例外が非線型です。線形とは「1次反応」であるということです。式で表すと以下になります。
-dX/dt = keX(一次反応の式は、物理化学まとめ 微分型速度式の積分型速度式への変換 参照。)
両辺を積分することで
lnC = -ket + lnC0 と表せます。すなわち、投与してから時間がどれくらい経てばどんな血中濃度になっているかがわかるということです。
横軸に時間、縦軸に血中薬物濃度 及び ln(血中薬物濃度)を取ったグラフは、それぞれ以下のようになります。
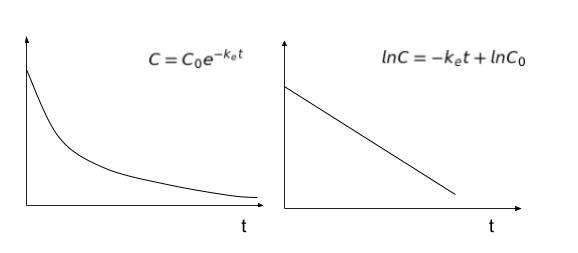
以上の内容は「静脈投与して1-コンパ」と仮定した場合の薬物の消失に関する話でした。経口1-コンパになるともう少し複雑になります。横軸に時間、縦軸に血中薬物濃度をとったグラフは以下のようになります。式を覚えるのは、不要。
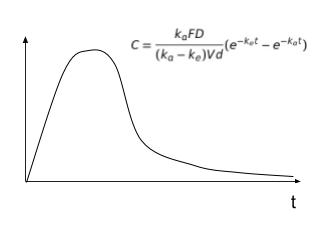

コメント