タンパク結合率が特徴的な(大きい or 小さい)薬物について、以下列挙します。
蛋白結合率が大きい薬物:シクロスポリン、タクロリムス、ワルファリン、プロフェン、プロプラノロール、アミオダロン、クロルプロマジン、ジギトキシンなど。
蛋白結合率が小さい薬物:リチウム、バンコマイシン、ゲンタマイシン、ジゴキシン、モルヒネ など。
この「タンパク結合率」をどう測定するかについて、以下詳しく説明します。タンパク結合率は、平衡透析法により計算することができます。平衡透析法とは、以下のような実験です。
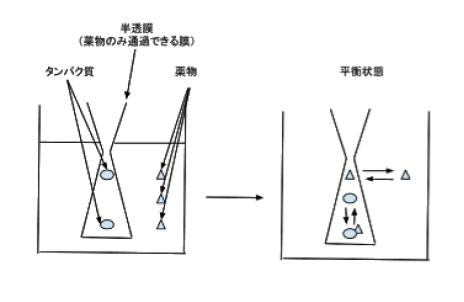
上図は、式で表すと「非結合薬物+タンパク質 ⇄ 結合型薬物」です。記号として非結合薬物を、free な Drug で、「fD」、タンパク質を、フリーな Protein なので 「fP」、結合型薬物をタンパク質と薬物の結合なので 「PD」と、以下表します。式を書き直すと 「fD + fP ⇄ PD」 です。
この関係において、平衡定数を「結合定数」と呼び K で表します。すると、 K = [PD]/[fD][fP] と書けます。この式を、いろんな工夫をしつつ変形すると、タンパク質 1 分子に薬物が何モル結合するかを r とした時、r を fD で表すことができます。
※ r = [PD]/[P] です。[P]は全タンパク質です。式で表すと[P]=[fP]+[PD] です。(参考ですが、r はタンパク質がもさっとあって薬物を入れて混ぜた時、タンパク質と薬物が結合する 確率を表し 0 ~ 1 の間をとる と考えるとイメージしやすいかもしれません。ただし、後の補足で、r は1以上の値も考えるのであくまでも理解のためのイメージとして参考にしてください。)
r を [fD] で表すことができると述べましたが、具体的な式は、以下のようになります。『r = nK[fD]/(1+K[fD]) 』です。これをラングミュア(Langmuir)式 と呼びます。この式の導出は、本項目の最後に補足としてあげます。余裕のある人は式の流れを追ってみてください。
ラングミュア式 では、横軸を [fD]、縦軸を r とする「ダイレクトプロット」の他、ダイレクトプロットが左辺を y 、[fD] を x とおけば「y = nx/1+x」 という式の形で、グラフにすると「曲線」なので少しわかりにくいことから。うまく横軸をとることでグラフを直線にすることができる「スキャッタードプロット」や「両辺逆数プロット」 をよく用います。それぞれのプロットにおいて傾きや、x 軸 y 軸との交点の座標が何を表すかを、導くか、覚えておくとよいです。
『スキャッタードプロット』は、式:r/[fD] = nK – rKです。縦軸に r/[fD]、 横軸に r をとります。傾きが、-K を表します。r = 0 の時の y 切片が nK を表します。r/[fD] = 0 の時、 r=n なので、x 切片が n を表します。
『両辺逆数プロット』では、式:1/r = 1/n + (1/nK)・[1/[fD]]です。縦軸に 1/r、横軸に 1/[fD] をとります。傾きが、 1/nK を表します。1/[fD] = 0 の時の、y 切片が 1/n を表します。1/r = 0 の時、1/[fD] = K なので、x 切片が -K を表します。
^^^以下、余裕がある人のみで OK^^^^
タンパク質と薬物の結合定数 からラングミュア式への導出は、以下の通りです。(式の変形をゆっくり追ってみてください。)※前提として[P]を、総タンパク質濃度 とします。いいかれると、[P] は、遊離しているタンパク質+薬物結合タンパク質の濃度 です。式で表すと[P]=[fP]+[PD]・・・(1)
(1)を変形すると、[fP]=[P]-[PD] ・・・(1)’ となります。これを結合定数の式 K = [PD]/[fD][fP] に代入します。
→K=[PD]/ [fD]([P]-[PD]) ・・・(2)となります。[PD] だけ2個あるから、[PD] について整理することを目標とします。分数のままだとよくわからないので、両辺に [fD]([P]-[PD]) をかけて分数じゃない式にしてみます。
K [fD] ([P]-[PD]) = [PD] ・・・(3)です。
次に、[PD]が関与する項を、右に集めます。
K [fD] [P] = (1+K[fD])[PD] ・・・(3)’
左右を交換します。
(1+K[fD])[PD] = K [fD] [P] ・・・(3)’’
両辺を(1+K[fD])で割ると、[PD] = ・・・になります。
[PD]= K[fD][P] /(1+K[fD])・・・(4)
両辺を [P] で割ります。
[PD]/[P]= K[fD] /(1+K[fD]) ・・・(5)
うまく、右辺は[fD] のみで表すことができました♪
※ 薬物の結合部位が1つのタンパク質に n 個ある場合はタンパク質 1 mol に、n 倍薬物が結合すると考えられます。従って、右辺を n 倍して
『r = [PD]/[P]= nK[fD] /(1+K[fD])』 となります。終わり。
^^^以上、余裕がある人のみで OK^^^^

コメント