エタン・ブタンの立体配座と安定性

分子内の二重結合や三重結合または環構造の場合、その結合はたやすく回転することができません。一方で単結合の場合は、その結合を自由に回転させることができます。

しかし、回転によって生じる原子の空間配置は様々で、空間的に有利な場合も不利な場合もあります。この空間配置のことを立体配座といい、空間的な有利・不利の度合いが、立体配座の安定性です。

エタンの立体配座

エタンは分子式CH₃-CH₃で表されるように、メチルとメチルが単結合でつながった構造をしています。その単結合の状態によって、例えば以下のような構造が書けます。

図1．エタンの重なり形配座　　図2．エタンのねじれ形配座

単結合は自由に回転させてよいので、図1のエタンのC-C結合を60°回転させると、図2のように表すことができます。

図1のNewman投影式を見るとHとHが重なっていることがわかります。原子（原子団）同士が近接していると、空間的に狭くなりエネルギー的に不利となります。これを「立体ひずみ」といいます。

一方、図2を見るとそれぞれのHは適度に離れていますので、こちらはエネルギー的に安定な配座となります。もちろん、図1と図2の間の配座も考えられますが、そのような配座の時はその安定性についても図1と図2の間となります。

また、図1のような状態を「重なり形」、図2のような状態を「ねじれ形」と呼んでいます。

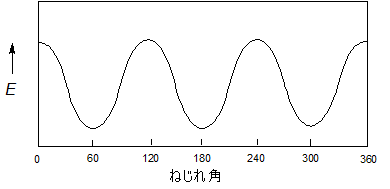
図3．エタンの回転によるポテンシャルエネルギー図の推移

ブタンの立体配座

ブタンについてもエタンと同じように考えることができますが、炭素数が多い分、少しだけ事情が異なります。先ほどと同様、以下にブタンのNewman投影式を記します。

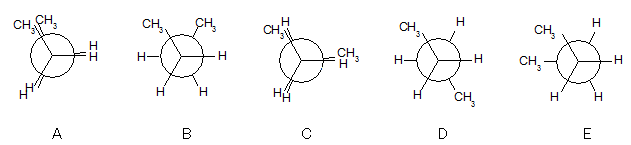
図4．ブタンのNewman投影図

図4のAの立体配座は、CH₃とCH₃が重なっていることがわかります。これは重なり形のため、エネルギー的に不安定です。この構造の単結合の前面を固定し、後方を時計回りに60°回転されるとBの配座になります。

さらに60°回すと再び重なり形になりますが、ここではCH₃とHが重なるため、先ほどのAの構造とは少し違ったCになります。そしてさらに60°回転させるとねじれ形（D）、次に120°回転させると、これもねじれ形（E）になります。

ここで、ともに重なり形であるAとCを見てください。2つの違いは前述の通り、Aの配座がCH₃とCH₃の重なりであるのに対し、Cの配座はCH₃とHとが重なっています。

原子（原子団）としてはHよりもCH₃のほうが大きいため、当然立体障害もAの配座のほうが大きくなり、結果としてより不安定になります。

今度はB,C,Dの配座に注目すると、こちらはいずれもねじれ型配座であることがわかります。

原子（原子団）同士が離れているためにどれも比較的安定ですが、BやEは2つのCH₃が隣同士に並んでいるのに対し、Dでは2つのCH₃が正反対に位置しています。よって、大きい原子団同士がより離れているDは、BやEよりも安定であるといえます。

このように、同じねじれ形でも置換基が相互に60°の位置に並ぶ場合と正反対（180°）の位置になる場合がありますが、前者をゴーシュ形、後者をアンチが形と呼んで使い分けています。

以上をまとめると、下の図5のようになります。

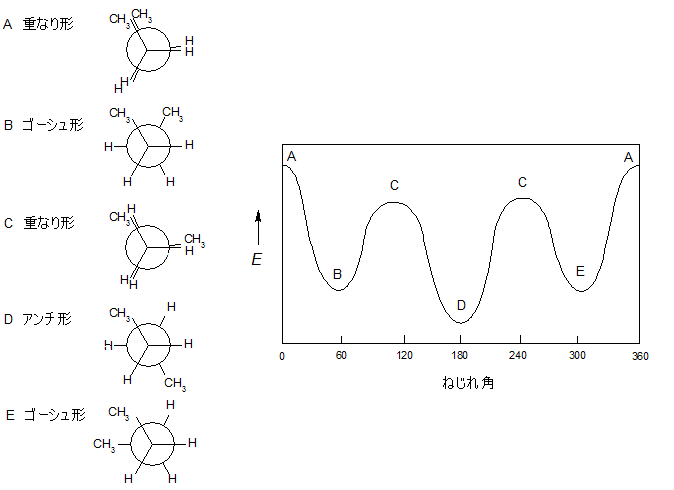
図5．ブタンの回転によるポテンシャルエネルギー図の推移