物質の溶解と速度

溶解とは、溶媒に気体、液体、固体が溶けて、均一な混合物である溶液になる現象のことです。以降、固体（薬物）の溶解について話をします。

固体の溶解においては、溶解熱の出入りを伴います。固体が溶媒中に溶解する量の上限値のことを溶解度と呼びますが、この溶解度は、温度と溶解熱の関数で表されます。すなわち、以下の式が成立します。

固体の溶解現象は、崩壊、分散を伴いながら溶解します。溶媒に溶け込む溶解速度は、大きい粒よりも顆粒が、顆粒よりも粉末の方が速いです。これは、溶媒と触れる表面積の量が大きいからです。

固体の溶解過程は、層状に、固体→飽和溶液→拡散層→内部溶液としてモデル化されます。このモデルに基づく式がNernst-Noyes-Whitney（ネルンスト・ノイエス・ホイットニー）の式　及び　Noyes-Whitney（ノイエス・ホイットニー）の式です。

すなわち、溶解現象が拡散律速であるとして拡散層を仮定し、溶解速度に関する種々のパラメータの関係を表す式です。以下のような式(Nernst-Noyes-Whitneyの式)になります。

上の式において、k = D/Vδ とおいた式が Noyes-Whitney の式です。以下の式になります。

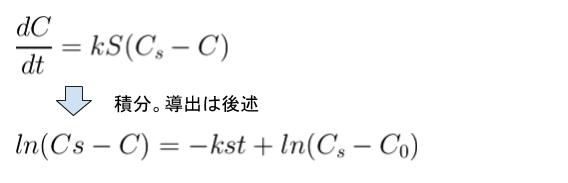
Noyes-Whitneyの式の微分型から積分型への導出は以下のようになります。Cs は溶解度なので、定数扱いであることに注意が必要です。

又、溶解による固体表面積の減少を考慮に入れた式が、Hixson-Crowell（ヒクソン－クロウェル）式です。Hixson-Crowell式では、２つの条件が仮定されています。すなわち、初期濃度が溶解度よりはるかに小さいこと（シンク条件と呼ばれます）と、粒子径一定の粒子が、球状を保ちつつ溶解するという仮定です。以下の式になります。

初期質量と、ある程度時間が経過した時の質量を測定することにより、k を求めることができるという点がポイントです。

補足　Hixon－Crowell　式の導出過程
※ 国試対策としては、全く不要です！

粒子の溶解のイメージは、以下のようになります。

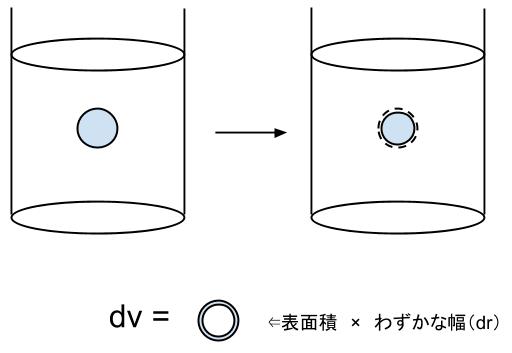
実際には、粒子は１個ではないので、N 個あるとすれば

　と表すことができます。

一方で、溶解現象なので、この節で解説した Nernst-Noyes-Whitney の式

も成り立ちます。この式から、少しアプローチします。

Cs＞＞Cという仮定をおくことにより、Cs－C　≒　Cs　とおきます。すると、以下の式になります。

少し、式の形を変形させると

　です。

この式の左辺　VdC は、(dV)C とすれば、（微小体積）×（濃度）なので減少した質量といえます。 つまり -dW = VdC です。一行にまとめると

となります。これで、dW と、t が、何か関係があるような式になってきました♪

次に、dW（質量の減少量） = ρdv（密度×減少した体積）　及び、S＝N × 4πr²（粒子がN個なので、N × 表面積　です）を代入すると、以下の式になります。

ここで、一番始めに表した式である

を用いて、式を簡単にします。ちょっと見た目を変えて

　としておきます。

すると

の形を変えて

とすれば、左辺を -dr とすることができるので

となります。

t = 0 → t = t
r = r0 → r = r 　の範囲で、上の式を積分すると

文字はいっぱいですが、結局積分する変数が、左辺にも、右辺にも入っていないので、１を x で積分したら x であるように、左辺は r 右辺は t をつけて定積分の計算になります。式は以下のようになります。

計算すると

　となります。

後は、この r₀ と ｒ を、W₀ 、W にすれば、終了です！

粒子径と、重さの間には、粒子が N 個なので

がなりたちます。これを、r について解きます。すると

※ r₀ = の時は、W₀ とします。これを代入すると

です。ほぼゴールです！形をあわせていきます。共通因数をくくりだします。

右辺の分母・分子に、3√（4ΠρN）δρをかけます。右辺は、√では無い方がわかりやすいので、指数で表します。

後は、定数部分の処理です。抜き出すと

　です。

分母を３（整数）にするために

何とかして、３６を３乗の形にするために

とすることで

となるので、定数項の処理も終わりです。