問 題
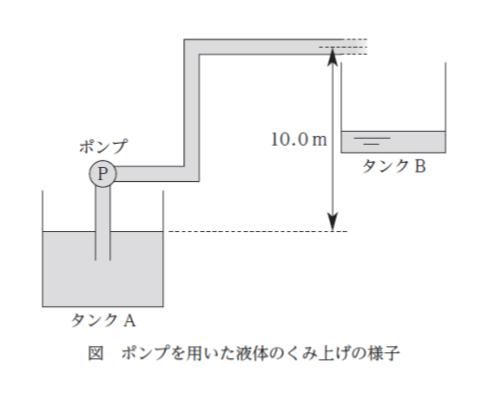
図のように、大気圧下でタンク A に入っている密度 1000 kg・m-3 の液体を、ポンプを用いて内径 20.0 cm の円管を通じてタンク B までくみ上げる。くみ上げる高さが 10.0 m、円管内の液体の平均流速が 2.00 m・s-1 で全摩擦損失が 100 J・kg-1 であったとき、ポンプによって液体に与えられた動力として最も妥当なのはどれか。
ただし、タンク A は十分に大きいので、液体をくみ上げても液面の位置は変化しないものとする。また、重力加速度の大きさを 9.8 m・s-2 とする。
1. 198 W
2. 200 W
3. 12400 W
4. 12600 W
5. 50300 W
正解.4
解 説
ポンプなので、ポンプの理論動力
P = ρgQH…(1) を思い出します。
連続の式 Q = Av から Q を求めます。
円管の断面積 A は、半径 10cm = 0.1m の円なので
A = π(0.1)2 = 0.01 π m2 です。
平均流速 v = 2.00 m/s なので
Q = 0.01π × 2.00
= 0.02π m3/s となります。
従って
(1) の右辺を計算すると
1000 × 9.8 × 0.02π × 10
= 1960π です。
実際には 損失分も動力が必要です。
全摩擦損失は 100 J/kg で
汲み上げる水の質量は 1000Q = 20π(kg/s) なので
2000 π (J) の摩擦損失があります。
1960π + 2000 π
≒ 4000 π とすれば
12566 W なので
最も近い選択肢を選ぶと 12600 W が妥当です。
以上より、正解は 4 です。

コメント